题目内容
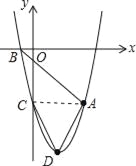
【题目】如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连接AB、BC、CD、DA,求四边形ABCD的面积.

【答案】(1)这条抛物线的表达式为y=x2-4x-5;(2) S四边形ABCD=18.
【解析】试题分析:(1)由二次函数图象上点的作伴特征可求出点C的坐标,结合OC=5OB即可得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出二次函数解析式;(2)将二次函数解析式变形为顶点式,由此即可得出点D的坐标,连接AC,将四边形ABCD分成两个三角形,再根据三角形的面积求出△ACB和△ACD的面积,将其相加即可得出结论.
试题解析:(1)∵抛物线y=ax2+bx﹣5(a≠0)与y轴交于点C, ∴点C的坐标为(0,﹣5),
∴OC=5, ∵OC=5OB, ∴OB=1. 又∵点B在x轴的负半轴上, ∴点B的坐标为(﹣1,0).
将A(4,﹣5),B(﹣1,0)代入y=ax2+bx﹣5中, 得:![]() ,解得:
,解得:![]() ,
,
∴这条抛物线的解析式是y=x2﹣4x﹣5.
(2)∵y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴顶点D的坐标为(2,﹣9), 连接AC,如图所示. ∵A(4,﹣5),C(0,﹣5),
∴AC∥x轴, ∴S△ABC=10,S△ACD=8, ∴四边形ABCD的面积=10+8=18.

练习册系列答案
相关题目


