Question

【题目】如图，点是正方形对角线上一动点，点在射线上，且，连接，为中点．

（1）如图1，当点在线段上时，试猜想与的数量关系和位置关系，并说明理由；

（2）如图2，当点在线段上时，（1）中的猜想还成立吗？请说明理由；

（3）如图3，当点在的延长线上时，请你在图3中画出相应的图形，并判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．

Answer 1

【答案】（1）且，详见解析；（2）猜想成立，详见解析；（3）猜想成立

【解析】

（1）根据点P在线段AO上时，利用三角形的全等判定和性质以及四边形内角和定理可以得出PE⊥PD，PE=PD；
（2）利用三角形全等得出，BP=PD，由PB=PE，得出PE=PD，要证PE⊥PD；从三方面分析，当点E在线段BC上（E与B、C不重合）时，当点E与点C重合时，点P恰好在AC中点处，当点E在BC的延长线上时，分别分析即可得出；
（3）根据题意作出图形，利用（2）中证明思路即可得出答案．

（1）当点P在线段AO上时，且，理由如下：
∵四边形是正方形，为对角线，

∴，，

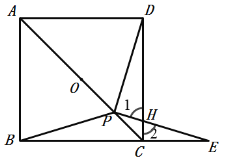
在△ABP和△ADP中，

，
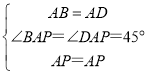∴△ABP≌△ADP，
∴，，，

又∵，

∴，，

∴，

∵，

∴，

∵正方形中，，

∴，

∴；

（2）当点在线段上时，且，理由如下：

∵四边形是正方形，为对角线，

∴，，

又，

∴，

∴，

又∵，

∴，

①当点与点重合时，；

②当点在的延长线上时，如图所示，

∵，

∴，

∴，

，

∴，

∴，

∵，

∴，

∴，

综上所述：．

∴当点在线段上时，（1）中的猜想成立；

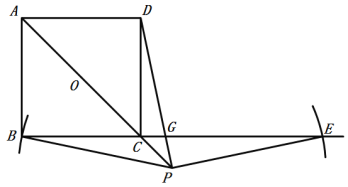
（3）当点在线段的延长线上时，如图所示，（1）中的猜想成立．

∵四边形是正方形，点在的延长线上，

∴，，

又，

∴，

∴，

又∵，

∴，

∵，

∴，

∴，

，

∴，

∴，

∵，

∴，

∴．