题目内容
【题目】如图,O是坐标原点,直线OA与双曲线![]() 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=![]() .
.
(1)求双曲线的解析式;
(2)直线AC与y轴交于点C(0,1),与x轴交于点D,求D点的坐标.

【答案】(1)![]() ; (2)D(-4,0)
; (2)D(-4,0)
【解析】试题分析:(1)根据正切的定义得到![]() ,而OB=4,得到AB=2,则A点坐标为(4,2),然后把A(4,2)代入
,而OB=4,得到AB=2,则A点坐标为(4,2),然后把A(4,2)代入![]() 即可求出k,从而确定双曲线的解析式;
即可求出k,从而确定双曲线的解析式;
(2)先利用待定系数法求出直线AC的解析式,然后确定D点坐标.
试题解析:解:(1)∵AB⊥x轴,OB=4,tan∠AOB=![]() ,∴
,∴![]() ,∴AB=2,∴A点坐标为(4,2),把A(4,2)代入
,∴AB=2,∴A点坐标为(4,2),把A(4,2)代入![]() 得,k=4×2=8,∴双曲线的解析式为
得,k=4×2=8,∴双曲线的解析式为![]() ;
;
(2)设直线AC的解析式为y=kx+b,把A(4,2)、C(0,1)代入得,4k+b=2,b=1,解得k=![]() ,b=1,∴直线AC的解析式为y=
,b=1,∴直线AC的解析式为y=![]() x+1,令y=0,则
x+1,令y=0,则![]() x+1=0,解得x=﹣4,∴D点坐标为(﹣4,0).
x+1=0,解得x=﹣4,∴D点坐标为(﹣4,0).

练习册系列答案
相关题目
【题目】如图,已知R t△ABC,∠ABC=90°,以直角边AB为直径作O,交斜边AC于点D,连结BD.
(1)若AB=3,BC=4,求边BD的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.

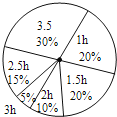
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.