题目内容
 16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.
16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.(1)求证:DE是⊙O的切线.
(2)若OB=5,BC=6,求CE的长.
分析:(1)要证明DE是⊙O的切线只要证明OD⊥DE即可;
(2)由已知利用勾股定理可求得OF的长,从而求得DF的长,由于四边形DECF是矩形那么CE的值就得到了.
(2)由已知利用勾股定理可求得OF的长,从而求得DF的长,由于四边形DECF是矩形那么CE的值就得到了.
解答: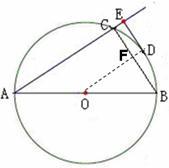 证明:(1)连接OD交BC于F;
证明:(1)连接OD交BC于F;
∵D为弧BC的中点,
∴OD⊥BC,
∵AB为直径,
∴∠ACB=90°;
又∵DE⊥AC,
∴∠CED=∠ECF=∠CFD=90°,
∴∠FDE=Rt∠即OD⊥DE;
又∵OD为⊙O的半径,
∴DE是⊙O的切线.
解:(2)∵OD⊥BC,BC=6,
∴BF=CF=3,
在Rt△OBF中,OB=5,BF=3,
∴OF=4,
∴DF=OD-OF=1;
又∵四边形DECF是矩形,
∴CE=DF=1.
答:CF的长是1.
 证明:(1)连接OD交BC于F;
证明:(1)连接OD交BC于F;∵D为弧BC的中点,
∴OD⊥BC,
∵AB为直径,
∴∠ACB=90°;
又∵DE⊥AC,
∴∠CED=∠ECF=∠CFD=90°,
∴∠FDE=Rt∠即OD⊥DE;
又∵OD为⊙O的半径,
∴DE是⊙O的切线.
解:(2)∵OD⊥BC,BC=6,
∴BF=CF=3,
在Rt△OBF中,OB=5,BF=3,
∴OF=4,
∴DF=OD-OF=1;
又∵四边形DECF是矩形,
∴CE=DF=1.
答:CF的长是1.
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
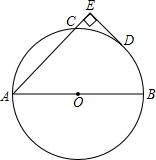 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.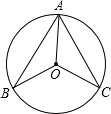 如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO=
如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO= (2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为
(2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为 如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.
如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.