Question

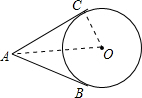
（2008•宝山区二模）如图，已知AB、AC是⊙O的两条切线，切点分是点B、点C，∠BAC=60°，又⊙O的半径为2cm，则点A与点O的距离为

4

cm．

Answer 1

分析：连接OC，OA，由AC为圆的切线，根据切线的性质得到OC与AC垂直，再由AC，AB为圆O的两条切线，根据切线长定理得到AO为∠BAC的平分线，根据∠BAC的度数求出∠CAO=30°，在直角三角形AOC中，由30°角所对的直角边等于斜边的一半，可得AO=2OC，由OC的长即可求出OA的长，即为点A与点O的距离．

解答：解：连接OC，OA，
∵AC，AB为圆O的切线，
∴OC⊥AC，AO为∠BAC的平分线，
又∠BAC=60°，
∴∠CAO=∠BAO=

1

2

∠BAC=30°，
在Rt△AOC中，OC=2cm，∠CAO=30°，
∴AO=2CO=4cm．
故答案为：4．

点评：此题考查了切线的性质，切线长定理，以及含30°角直角三角形的性质，熟练掌握性质及定理是解本题的关键．同时注意已知切线，连接圆心与切点这条辅助线的做法．