题目内容
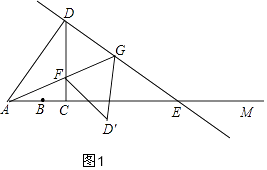
【题目】如图,射线AM上有一点B,AB=6,点C是射线AM上异于B的一点,过C作CD⊥AM,且CD= ![]() AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
AC,过D点作DE⊥AD,交射线AM于E,在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G,设AC=3x.
(1)当C在B点右侧时,求AD.DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形;
(3)作点D关于AG的对称点D′,连接FD′,GD′,若四边形DFD′G是平行四边形,求x的值.(直接写出答案)
【答案】
(1)
解:∵CD= ![]() ,AC=3x,
,AC=3x,
∴CD=4x,
∵CD⊥AM,
∴∠ACD=90°,
由勾股定理得:AD=5x,
∵AB=6,C在B点右侧,
∴BC=AC﹣AB=3x﹣6,
∵BC=FC=3x﹣6,
∴DF=CD﹣FC=4x﹣(3x﹣6)=x+6
(2)
解:分两种情况:
①当C在B点的右侧时,
∴AC>AB,
∴F必在线段CD上,
∵∠ACD=90°,
∴∠AFD是钝角,若△ADF为等腰三角形,只可能AF=DF,过F作FN⊥AD于N,如图2,

∴AN=ND=2.5x,
cos∠ADC= ![]() =
= ![]() ,
,
![]() ,
,
x= ![]() ;
;
②当C在线段AB上时,同理可知若△ADF为等腰三角形,只可能AF=DF,
i)当CF<CD时,过F作FN⊥AD于N,如图3,

∵AB=6,AC=3x,
∴BC=CF=6﹣3x,
∴DF=4x﹣(6﹣3x)=7x﹣6,
cos∠ADC= ![]() ,
,
∴ ![]() ,
,
x= ![]() ,
,
ii)当CF>CD时,如图4,
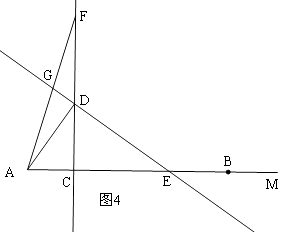
BC=CF=6﹣3x,
∴FD=AD=6﹣3x﹣4x=6﹣7x,
则6﹣7x=5x,
x= ![]() ,
,
综上所述,当x= ![]() 或
或 ![]() 或
或 ![]() 时,△AFD是等腰三角形
时,△AFD是等腰三角形
(3)
解:∵四边形DFD′G是平行四边形,且DF=D′F,
∴DFD′G是菱形,
∴DF=DG,
∴∠DFG=∠DGF,
∵∠AFC=∠DFG,
∴∠DGF=∠AFC,
∵∠ACD=∠ADG=90°,
∴∠FAC=∠DAG,
即AF平分∠DAC,
过F作FN⊥AD于N,
当C在AB的延长线上时,如图2,

FN=FC=3x﹣6,DF=x+6,
sin∠CDA= ![]() ,
,
解得:x=4,
当C在AB边上时,如图5,
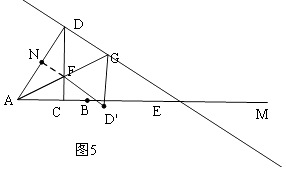
FN=FC=6﹣3x,
DF=7x﹣6,
sin∠CDA= ![]() =
= ![]() ,
,
x= ![]() ,
,
综上所述,若四边形DFD′G是平行四边形,x的值是4或 ![]()
【解析】(1)由已知条件可得:CD=4x,根据勾股定理得:AD=5x,由AB=6且C在B点右侧,可以依次表示BC、CF、DF的长;(2)分两种情况:①当C在B点的右侧时,AF=DF,②当C在线段AB上时,又分两种情况:i)当CF<CD时,如图3,ii)当CF>CD时,如图4,由AF=DF,作等腰三角形的高线FN,由等腰三角形三线合一得:AN=ND=2.5x,利用同角的三角函数列比例式可求得x的值;(3)先根据四边形DFD′G是平行四边形证明它为菱形,由角的关系得:AF平分∠DAC,作辅助线,由角平分线的性质得:FN=FC,根据第2问分两种情况进行计算,根据同角的三角函数列式可求得x的值.

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多? A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |



