题目内容

如图，△ABC是正三角形，曲线CDEFG…叫做“正三角形的渐开线”，曲线的各部分为圆弧．
（1）图中已经有4段圆弧，请接着画出第5段圆弧GH；
（2）设△ABC的边长为a，则第1段弧的长是
 
，第5段弧的长是
 
．前5段弧长的和（即曲线CDEFGH的长）是
 
；
（3）类似地有“正方形的渐开线”，“正五边形的渐开线”，…，边长为a的正方形的渐开线的前5段弧长的和是
 
；
（4）猜想，①边长为a的正n边形的前5段弧长的和是
 
；
②边长为a的正n边形的前m段弧长的和是
 
．
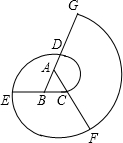
精英家教网
分析：（1）以点B为圆心，BG长为半径画弧即可；
（2）利用弧长公式计算．但要先确定弧所对的圆心角都是120度，半径却在不断的增大，第一次是1，第二次是2，第三次是3，依此下去第五次是5，总和就是把五段弧加起来．
（3）先利用五边形的性质求出五边形的外角度数，再利用弧长公式计算；
（4）五段弧相加，利用多边形的外角公式和弧长公式进行计算．
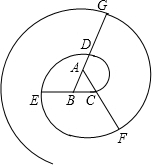
解答：解：（1）如右图（1分）
精英家教网

（2）
2
3
πa，
10
3
πa，10πa；（3分）

（3）
15πα
2
；（2分）

（4）
30
n
πa，
m(m+1)
n
πa．（（2分）+2分））
点评：本题主要考查了弧长公式及多边形的内角和及外角的计算方法，学生注意在做题时要把所学的各块的知识给系统起来．
练习册系列答案
相关题目
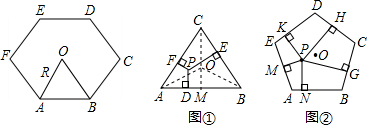（2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
探索发现：
（1）为了解决这个问题，我们不妨从最简单的正多边形--正三角形入手．
如图①，△ABC是正三角形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距离分别为h1、h2、h3 ，确定h1+h2+h3的值与△ABC的半径R及中心角的关系．
解：设△ABC的边长是a，面积为S，显然S=
1
2
a（h1+h2+h3）
O为△ABC的中心，连接OA、OB、OC，它们将△ABC分成三个全等的等腰三角形，过点O作OM⊥AB，垂足为M，Rt△AOM中，易知
OM=OAcos∠AOM=Rcos
1
2
∠AOB=Rcos
1
2
×120°=Rcos60°，
AM=OAsin∠AOM=Rsin
1
2
∠AOB=Rsin
1
2
×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S△AOB=
1
2
AB×OM=
1
2
×2Rsin60°•Rcos60°=R2sin60°cos60°
∴S△ABC=3S△AOB=3R2sin60°cos60°
∴
1
2
a（h1+h2+h3）=3R2sin60°cos60°
即：
1
2
×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°
∴h1+h2+h3=3Rcos60°
（2）如图②，五边形ABCDE是正五边形，半径是R，P是正五边形ABCDE内任意一点，P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5，参照（1）的探索过程，确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系．
（3）类比上述探索过程，直接填写结论
正六边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=
6Rcos30°
6Rcos30°

正八边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=
8Rcos22.5°
8Rcos22.5°

正n边形（半径是R）内任意一点P到各边距离之和  h1+h2+…+hn=
nRcos
180°
n
nRcos
180°
n
．
如图，△ABC是正三角形，曲线CDEFG…叫做“正三角形的渐开线”，其中
CD
、
DE
、
EF
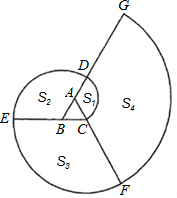、…的圆心精英家教网依次为A、B、C…．当渐开线延伸开时，形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1．
（1）求出曲线CDEFG的总长度．
（2）求出扇环S4的面积．
如图，在直角坐标系xOy中，直线AB交x轴于A（1，0），交y轴负半轴于B（0，-5），C为x轴正半轴上一点，且CA=
4
5
CO．
（1）求△ABC的面积．
（2）延长BA到P，使得PA=AB，求P点的坐标．
（3）如图，D是第三象限内一动点，且OD⊥BD，直线BE⊥CD于E，OF⊥OD交BE延长线于F．当D点运动时，
OD
OF
的大小是否发生变化？若改变，请说明理由；若不变，求出这个比值．
如图，△ABC是一个电子跳蚤游戏盘，其中AB=6，AC=7，BC=8．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第一次落点）处，且CP1=CP0；第二步从P1跳到AB边的P2（第二次落点）处，且AP2=AP1；第三步从P2跳到BC边的P3（第三次落点）处，且BP3=BP2；…；跳蚤按上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P1与P2014之间的距离为（　　）
如图，△ABC是正三角形，曲线CDEFG…叫做“正三角形的渐开线”，其中的圆心依次为A、B、C…．当渐开线延伸开时，形成三个扇形S1、S2、S3和一系列扇环S4、S5、…若正△ABC的边长为1．
（1）求出曲线CDEFG的总长度．
（2）求出扇环S4的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网