题目内容
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]=________,<3.5>=________.
(2)若[x]=2,则x的取值范围是________;若<y>=﹣1,则y的取值范围是________.
(3)已知x,y满足方程组 ,求x,y的取值范围.
,求x,y的取值范围.
【答案】(1)﹣5;4;(2)2≤x<3;﹣2≤y<﹣1(3)﹣1≤x<0,2≤y<3
【解析】试题分析:(1)根据题目条件:用[a]表示不大于a的最大整数,用<a>表示大于a的最小整数,可分别求解;(2)根据[a]表示不大于a的最大整数,可得[x]=2中的2≤x<3,根据<a>表示大于a的最小整数,可得<y>=-1中,-2≤y<-1;(3)先解方程组,求出[x]和<y>的值,然后求出x和y的取值范围.
试题解析:1)由题意得,[-4.5]=-5,<3.5>=4;
(2)因为[a]表示不大于a的最大整数且[x]=2,所以x的取值范围是2≤x<3;
因为<a>表示大于a的最小整数,且<y>=-1, 所以y的取值范围是-2≤y<-1;
(3)解:解方程组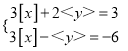 得:
得: ![]() ,
,
∴x,y的取值范围分别为﹣1≤x<0,2≤y<3

练习册系列答案
相关题目
【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A | B | |
载客量(人/辆) | 40 | 20 |
租金(元/辆) | 200 | 150 |
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?


