Question

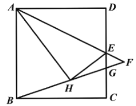
【题目】如图，在正方形中，，点是的中点，连接，将沿折叠至，连接，延长，交于点；，交于点，则______．

Answer 1

【答案】

【解析】

过点H作MN∥AD，交AB于M，交CD于N，通过证明△AMH∽△HNE，可得，可得MH＝2EN，HN＝，可求EN的长，即可求BM，MH，HN的长，由平行线分线段成比例可得HG，GN，EG，GF的长．

解：过点H作MN∥AD，交AB于M，交CD于N，

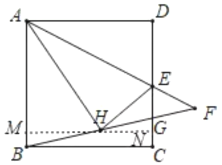
∴∠BAD＝∠BMN＝90°，∠D＝∠MNC＝90°，
∴四边形ADNM是矩形，
∴AM＝DN，MN＝AD＝2，
∵将△ADE沿AE折叠至△AHE，且E是DC的中点，
∴AH＝AD＝2，∠AHE＝90°，HE＝DE＝1，
∴∠AHM＋∠EHN＝90°，且∠MAH＋∠AHM＝90°，
∴∠MAH＝∠EHN，且∠AMH＝∠ENH＝90°，
∴△AMH∽△HNE，

∴，

∴，

∴MH＝2EN，HN＝，

∵MH＋HN＝MN＝2，

∴，

解得：，

∴MN=，HN=，AM=，

∴BM=，

∴BH=，

∵AB∥CD，

∴，

∴，

∴BG=，EG=，

∵AB∥CD，

∴，

即，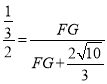

解得：，

故答案为：