题目内容
【题目】已知△ABC内接于⊙O,过点A作直线EF.

(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
【答案】(1)①∠BAE=90°,②∠EAC=∠ABC
(2)EF是⊙O的切线
【解析】
试题分析:(1)添加条件EF⊥AB,根据切线的判定推出即可;添加条件∠EAC=∠B,根据直径推出∠CAB+∠B=90°,推出∠EAC+∠CAB=90°,根据切线判定推出即可;
(2)作直径AM,连接CM,推出∠M=∠B=∠EAC,求出∠EAC+∠CAM=90°,根据切线的判定推出即可.
试题解析:(1)①∠BAE=90°,②∠EAC=∠ABC,
理由是:①∵∠BAE=90°,∴AE⊥AB, ∵AB是直径,∴EF是⊙O的切线;
②∵AB是直径,∴∠ACB=90°,∴∠ABC+∠BAC=90°,
∵∠EAC=∠ABC,∴∠BAE=∠BAC+∠EAC=∠BAC+∠ABC=90°,即AE⊥AB,
∵AB是直径,∴EF是⊙O的切线;
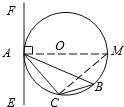
(2)EF是⊙O的切线.
作直径AM,连接CM,则∠ACM=90°,∠M=∠B,
∴∠M+∠CAM=∠B+∠CAM=90°,
∵∠CAE=∠B,∴∠CAM+∠CAE=90°,∴AE⊥AM,
∵AM为直径,∴EF是⊙O的切线.

 名校课堂系列答案
名校课堂系列答案【题目】某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:

(1)计算并完成表格:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 |
(2)假如你去转动该转盘一次,你获得铅笔的概率约是多少?

