题目内容
【题目】两个完全相同的正四面体骰子的各面上分别标明数字1,2,3,4,在桌子上同时投掷这两个正四面体骰子,请用列表法或画树状图的方法,求与桌面接触的面所得的点数之和等于6的概率.
【答案】![]()
【解析】试题分析:
如果采用列表法,那么可以将每枚骰子可能出现的点数分别在纵横两个方向上依次列出,并按照表格的结构依次填写各种可能的组合情况. 如果采用树状图法,那么可以将第一枚骰子的情况作为第一层,第二枚骰子的情况作为第二层,先在第一层上列出可能出现的点数,再根据树状图的特点和第二枚骰子可能出现的点数完成第二层. 分析上述的表或树状图,统计所有可能的情况以及所求事件的可能情况的数量,利用概率计算公式求得相应的概率.
试题解析:
(1) (列表法)
根据题意列表如下.
第一枚骰子 第二枚骰子 | 1 | 2 | 3 | 4 |
1 | (1, 1) | (2, 1) | (3, 1) | (4, 1) |
2 | (1, 2) | (2, 2) | (3, 2) | (4, 2) |
3 | (1, 3) | (2, 3) | (3, 3) | (4, 3) |
4 | (1, 4) | (2, 4) | (3, 4) | (4, 4) |
由上表可以看出,共有16种情况,其中两个骰子与桌面接触的面所得的点数之和等于6的情况共有3种.
∴P(与桌面接触的面所得的点数之和等于6)= ![]() .
.
(2) (树状图法)
根据题意画出如下图所示的树状图.
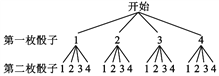
由上面的树状图可以看出,共有16种情况,其中两个骰子与桌面接触的面所得的点数之和等于6的情况共有3种.
∴P(与桌面接触的面所得的点数之和等于6)= ![]() .
.

练习册系列答案
相关题目