题目内容
【题目】已知:如图,三角形ABC中,D是BC边上一点.
(1)过点D作AB、AC的平行线分别交AB于点E,交AC于点F;
(2)说明:∠EDF=∠A;
(3)说明:∠A+∠B+∠C=180°.

【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】
(1)利用直尺过点D作DE∥AC交AB于E,过点D作DF∥AB交AC于F即可;
(2)由AB∥DF,AC∥DE知∠A+∠AED=180°,∠EDF+∠AED=180°,据此可得;
(3)由AB∥DF,AC∥DE知∠B=∠FDC,∠C=∠BDE,根据∠BDE+∠EDF+∠FDC=180°及∠EDF=∠A可得.
解:(1)如图所示,DE、DF即为所求.
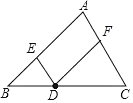
(2)∵AB∥DF,AC∥DE,
∴∠A+∠AED=180°,∠EDF+∠AED=180°,
∴∠A=∠EDF;
(3)∵AB∥DF,AC∥DE,
∴∠B=∠FDC,∠C=∠BDE,
由(2)知∠A=∠EDF,
∵∠BDE+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目