题目内容

【题目】如图，M是△ABC的边BC的中点，AN平分，BNAN于点N，延长BN交AC于点D，已知AB=10，AC=16.

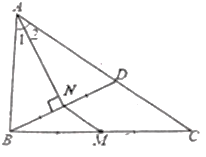
（1）求证：BN=DN；

（2）求MN的长.

【答案】（1）见详解；（2）3.

【解析】

（1）证明△ABN≌△ADN，即可得出结论；

（2）由（1）知AB=AD，则CD=，再判断MN是△BDC的中位线，从而得出MN=，即可得到答案.

证明：（1）∵AN平分∠BAC

∴∠1=∠2，

∵BN⊥AN

∴∠ANB=∠AND=90°，

在△ABN和△ADN中，

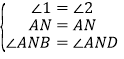
∴△ABN≌△ADN（ASA）

∴BN=DN；

（2）由（1）知，△ABN≌△ADN

∴AD=AB=10，DN=NB，

∴CD=AC-AD=16-10=6，

又∵点M是BC中点，

∴MN是△BDC的中位线，

∴MN=CD=3．

练习册系列答案
相关题目

【题目】某校随机抽取部分学生，就“学习习惯”进行调查，将“对自己做错题进行整理、分析、改正”（选项为：很少、有时、常常、总是）的调查数据进行了整理，绘制成部分统计图如下：

请根据图中信息，解答下列问题：

（1）该调查的样本容量为________， =________%， =________%，“常常”对应扇形的圆心角的度数为__________；

（2）请你补全条形统计图；

（3）若该校有3200名学生，请你估计其中“总是”对错题进行整理、分析、改正的

学生有多少名？

【题目】一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同，其中黄球的个数是白球个数的2倍少5个，已知从袋中摸出一个球是红球的概率是.

(1)求袋中红球的个数；

(2)求从袋中摸出一个球是白球的概率；

(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.

【题目】如图，在平面直角坐标系中， ，线段在轴上， =12，点的坐标为(-3,0)，线段交轴于点，过作于，动点从原点出发，以每秒3个单位的速度沿轴向右运动，设运动的时间为秒.

(1)点的坐标为（_________），__________);

(2)当是等腰三角形时，求的值;

(3)若点运动的同时， 以为位似中心向右放大，且点向右运动的速度为每秒2个单位， 放大的同时高也随之放大，当以为直径的圆与动线段所在直线相切，求的值和此时C点的坐标.

【题目】已知函数y＝的图象如图所示，则以下结论：①m＜0；②在每个分支上y随x的增大而增大；③若点A(－1，a)，点B(2，b)在图象上，则a ＜b；④若点P(x，y)在图象上，则点P1(－x，y)也在图象上．其中正确的个数为(　　)

A. 4 B. 3 C. 2 D. 1

【题目】已知二次函数y=ax2+bx+c（a≠0，a、b、c为常数）的图象如图所示，下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④c＜4b；⑤a+b＜k（ka+b）（k为常数，且k≠1）．其中正确的结论有（ ）

A. 2个 B. 3个 C. 4个 D. 5个

【题目】已知，数轴上三个点A、O、P，点O是原点，固定不动，点A和B可以移动，点A表示的数为，点B表示的数为.

（1）若A、B移动到如图所示位置，计算的值.

（2）在（1）的情况下，B点不动，点A向左移动3个单位长，写出A点对应的数，并计算.

（3）在（1）的情况下，点A不动，点B向右移动15.3个单位长，此时比大多少？请列式计算.

【题目】如图所示，在菱形纸片ABCD中，AB＝4，∠BAD＝60°，按如下步骤折叠该菱形纸片：

第一步：如图①，将菱形纸片ABCD折叠，使点A的对应点A′恰好落在边CD上，折痕EF分别与边AD、AB交于点E、F，折痕EF与对应点A、A′的连线交于点G．

第二步：如图②，再将四边形纸片BCA′F折叠使点C的对应点C′恰好落在A′F上，折痕MN分别交边CD、BC于点M、N．

第三步：展开菱形纸片ABCD，连接GC′，则GC′最小值是_____．

【题目】在△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c.

(1)已知c＝8，∠A＝60°，求∠B，a，b；

(2)已知a＝3，∠A＝45°，求∠B，b，c.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网