题目内容
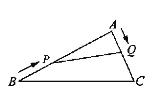
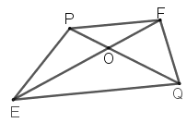
【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
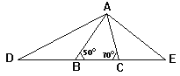
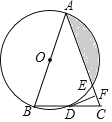
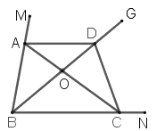
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
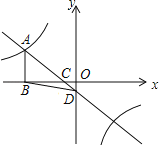
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
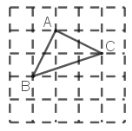
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
【答案】(1)见解析;(2)4;(3)∠ADC的度数为125°或110°.
【解析】
(1)根据平行线的性质和角平分线的性质可得△ABD是等腰三角形,然后可求出∠ABD=∠ADB=∠DBC=40°,利用三角形内角和定理求出∠BDC的度数即可得到△BCD为等腰三角形,即点C是△ABD的“同类点”;
(2)找出所有在BC下方能使△BCD为等腰三角形的格点D即可;
(3)根据点C为△ABD的“同类点”可知△BCD为等腰三角形,然后分情况讨论:①当BD=BC时,②当BC=CD时,分别作出图形,根据等边三角形的判定和性质以及等腰三角形的性质求解即可.
解:(1)∵BG平分∠MBN,
∴∠ABD=∠DBC,
∵AD∥BN,
∴∠ADB=∠DBC,
∴∠ADB=∠ABD,
∴△ABD是等腰三角形,
又∵∠BAD=100°,
∴∠ABD=∠ADB=∠DBC=40°,
∵∠BCD=70°,
∴∠BDC=180°-∠DBC-∠BCD=180°-40°-70°=70°,
∴△BCD为等腰三角形,
∴点C是△ABD的“同类点”;
(2)如图所示:这样的点D共有4个;
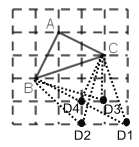
(3)∵∠ABC=110°,DA=AB=BC,BD≠CD,点C为△ABD的“同类点”,
分情况讨论:
①如图,当BD=BC时,则BD=BC=DA=AB,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
∴∠DBC=110°-60°=50°,
∴∠BDC=![]() ,
,
∴∠ADC=∠ADB+∠BDC=60°+65°=125°;

②如图,当BC=CD时,
则∠ABD=∠ADB,∠CDB=∠CBD,
∴∠ADB+∠CDB=∠ABD+∠CBD,
∴∠ADC=∠ABC=110°,
综上,∠ADC的度数为125°或110°.

【题目】幻方是一种将数字排在正方形格子中,使每行、每列和每条对角线上的数字和都相等的模型.数学课上,老师在黑板上画出一个幻方如图所示,并设计游戏:一人将一颗能粘在黑板上的磁铁豆随机投入幻方内,另一人猜数,若所猜数字与投出的数字相符,则猜数的人获胜,否则投磁铁豆的人获胜.猜想的方法从以下两种中选一种:
|
|
|
|
|
|
|
|
|
![]() 猜“是大于
猜“是大于![]() 的数”或“不是大于
的数”或“不是大于![]() 的数”;
的数”;
![]() 猜“是
猜“是![]() 的倍数”或“不是
的倍数”或“不是![]() 的倍数”;
的倍数”;
如果轮到你猜想,那么为了尽可能获胜,你将选择哪--种猜数方法?怎么猜?为什么?