Question

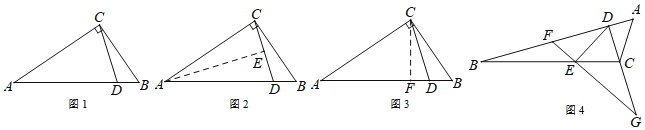
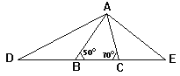
【题目】如图,若△ABC的∠ABC＝50°,∠ACB＝70°，延长CB至点D,使BD＝BA,延长BC至E点,使CE＝CA, 连接AD、AE,则∠DAE的度数为__________度.

Answer 1

【答案】120

【解析】

由题意知△ABD和△ACE均为等腰三角形，可由三角形内角和定理求得∠BAC的度数，用三角形外角的性质求得∠DAB与∠CAE的度数，即可求得∠DAE的度数．

解：∵∠ABC＝50°，∠ACB＝70°，

∴∠BAC＝180°∠ABC∠ACB＝180°50°70°＝60°，

∵BD＝BA，

∴∠D＝∠DAB＝∠ABC＝25°，

∵CE＝CA，

∴∠E＝∠CAE＝∠ACB＝35°，

∴∠DAE＝∠DAB＋∠BAC＋∠CAE＝25°＋60°＋35°＝120°，

故答案为：120.