题目内容
【题目】两个反比例函数y=![]() ,y=
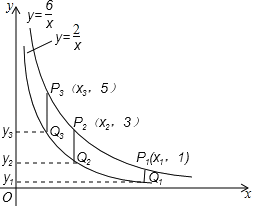
,y=![]() 在第一象限内的图象如图所示,点P1,P2,P3…,P2017在反比例函数y=
在第一象限内的图象如图所示,点P1,P2,P3…,P2017在反比例函数y=![]() 图象上,它们的横坐标分别是x1,x2,x3…,x2017,纵坐标分别是1,3,5,…,共2017个连续奇数,过点P1,P2,P3,…P2017分别作y轴的平行线,与y=
图象上,它们的横坐标分别是x1,x2,x3…,x2017,纵坐标分别是1,3,5,…,共2017个连续奇数,过点P1,P2,P3,…P2017分别作y轴的平行线,与y=![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),则y2017=_____.
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),则y2017=_____.
【答案】![]()
【解析】
找出第2017个奇数,利用反比例函数图象上点的坐标特征即可求出点P2017的坐标,由P2017Q2017∥y轴可得出x2017的值,再利用反比例函数图象上点的坐标特征即可求出y2017的值.
第2017个奇数为2×2017﹣1=4033,
∵当y=![]() =4033时,x=
=4033时,x=![]() ,
,
∴点P2017的坐标为(![]() ,4033).
,4033).
∵P2017Q2017∥y轴,
∴x2017=![]() .
.
∵当x=![]() 时,y=
时,y=![]() =
=![]() =
=![]() ,
,
∴点Q2017的坐标为(![]() ,
,![]() ).
).
故答案为:![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目