��Ŀ����
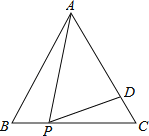
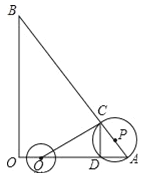
����Ŀ����ͼ������AOB�У���AOBΪֱ�ǣ�OA=6��OB=8���뾶Ϊ2�Ķ�ԲԲ��Q�ӵ�O����������OA������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�A����������AB����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�ΪC��D������CD��QC��
��1����tΪ��ֵʱ����Q���D�غϣ�
��2������Q������Aʱ�����P��OB�صõ��ҳ���
��3������P���߶�QCֻ��һ�������㣬��t��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3��0��t��
����3��0��t��![]() ��
��![]() ��t��5��
��t��5��
��������
��1��������֪CD��OA��������ACD�ס�ABO�����ö�Ӧ�ߵı����AD�ij��ȣ���Q��D�غ�ʱ����AD+OQ=OA���г����̼������t��ֵ��
��2������0��t��5����Q����A��ʱ��OQ=4����ʱ��ʱΪ4s������P��PE��OB�ڵ�E�����ô����������������P��OB�صõ��ҳ���
��3������P���߶�QCֻ��һ�������㣬�������������������QC����P����ʱ���������ʱ��ʱ�䣻����Q��D�غ�ʱ���������ʱ��ʱ�䣻����������������ɵó�t��ȡֵ��Χ��
��1����OA=6��OB=8��
���ɹ��ɶ�������ã�AB=10��
������֪��OQ=AP=t��
��AC=2t��
��AC����P��ֱ����
���CDA=90�㣬
��CD��OB��
���ACD�ס�ABO��
��![]() ��
��
��AD=![]() ��
��
��Q��D�غ�ʱ��
AD+OQ=OA��
��![]() +t=6��
+t=6��
��t=![]() ��
��
��2������Q����A��ʱ����ͼ

OQ=OA��QA=4��
��t=![]() =4s��
=4s��
��PA=4��
��BP=AB��PA=6��
����P��PE��OB�ڵ�E����P��OB�ཻ�ڵ�F��G��
����PF��
��PE��OA��
���PEB�ס�AOB��
��![]() ��
��
��PE=3.6��
���ɹ��ɶ�������ã�EF=![]() ��
��
�ɴ�����������֪��FG=2EF=![]() ��
��
��3����QC����P����ʱ����ͼ

��ʱ��QCA=90�㣬
��OQ=AP=t��
��AQ=6��t��AC=2t��
�ߡ�A=��A��
��QCA=��ABO��
���AQC�ס�ABO��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
����0��t��![]() ʱ����P��QCֻ��һ�����㣬
ʱ����P��QCֻ��һ�����㣬
��QC��OAʱ��
��ʱQ��D�غϣ�
�ɣ�1����֪��t=![]() ��
��
����![]() ��t��5ʱ����P��QCֻ��һ�����㣬
��t��5ʱ����P��QCֻ��һ�����㣬
����������������P��QCֻ��һ�����㣬t��ȡֵ��ΧΪ��0��t��![]() ��
��![]() ��t��5��
��t��5��