题目内容
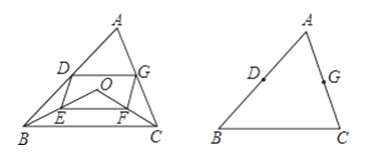
【题目】点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
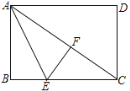
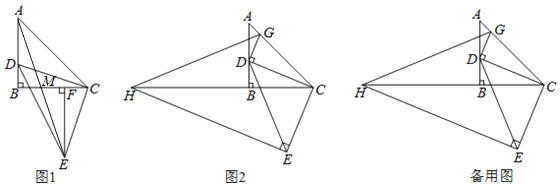
(1)如图,当点O在△ABC内时,求证:四边形DEFG是平行四边形;
(2)当点O在△ABC外时,(1)的结论是否成立?(画出图形,指出结论,不需说明理由;)
(3)若四边形DEFG是菱形,则点O的位置应满足什么条件?试说明理由.
【答案】(1)见解析;(2)成立,理由见解析;(3)当点O满足OA=BC,四边形DEFG是菱形,理由见解析
【解析】
(1)(2)根据平行四边形的判定性质求证.
(3)把结论当做已知条件,由结论推出已知.
证明:(1)∵AB、OB、OC、AC中点分别为D、E、F、G
∴DG、EF分别为△ABC和△OBC的中位线
∴DG∥BC,EF∥BC,DG=![]() BC,EF=
BC,EF=![]() BC
BC
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
(2)解:成立,
理由是:如图所示,
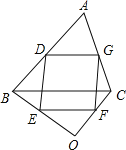
∵由(1)知,DG∥BC,EF∥BC,DG=![]() BC,EF=
BC,EF=![]() BC
BC
∴DG∥EF且DG=EF
∴四边形DEFG是平行四边形;
(3)当点O满足OA=BC,四边形DEFG是菱形.
由三角形中位线性质得DE=EF,
所以平行四边形DEFG是菱形.

练习册系列答案
相关题目