题目内容
已知：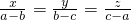
，求证x+y+z=0．
解：设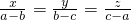=k，
则x=ka-kb，y=kb-kc，z=kc-ka，
x+y+z=ka-kb+kb-kc+kc-ka=0，
∴x+y+z=0．
分析：设恒等式等于一个常数，求出x，y，z与这个常数的关系式，再进行证明．
点评：设出恒等式等于一个常数，求出x，y，z与这个常数的关系式是解答本题的关键．
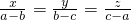=k，则x=ka-kb，y=kb-kc，z=kc-ka，
x+y+z=ka-kb+kb-kc+kc-ka=0，
∴x+y+z=0．
分析：设恒等式等于一个常数，求出x，y，z与这个常数的关系式，再进行证明．
点评：设出恒等式等于一个常数，求出x，y，z与这个常数的关系式是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
28、阅读下面的证明过程，指出其错误．
27、已知△ABC，求证：∠A+∠B+∠C=180°．
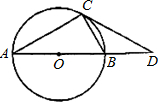如图，△ABC内接于⊙O，AB是⊙O的直径，延长AB到D，连接CD．请你结合图形，编写一道题．要求：再补充两个已知条件，并写出在所有已知条件下得出的一个结论．例如：
28、仅通过观察、试验等可以寻找规律，但是由于观察可能有误差，这样仅通过观察、试验等就下结论有时也缺乏说服力，所以得出的结论还需要证明．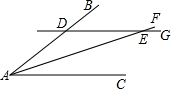
如图，点D在AB上，直线DG交AF于点E．请从①DG∥AC，②AF平分∠BAC，③AD=DE中任选两个作为条件，余下一个作为结论，构造一个真命题，并说明理由．已知：