Question

28、阅读下面的证明过程，指出其错误．
已知△ABC．
求证：∠A+∠B+∠C=180度．
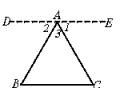
证明：过A作DE∥BC，且使∠1=∠C
∵DE∥BC（画图）
∴∠2=∠B（两直线平行，内错角相等）
∵∠1=∠C（画图）
∴∠B+∠C+∠3=∠2+∠1+∠3=180°
即∠BAC+∠B+∠C=180°

Answer 1

分析：注意作辅助线的方法，不能同时让它满足两个条件．只能作平行线后，根据平行线的性质得到角相等．

解答：解：错误：过A作DE∥BC，且使∠1=∠C，应改为：过A作DE∥BC．∵∠1=∠C（画图），应改为∴∠1=∠C（两直线平行，内错角相等）．
证明：过A作DE∥BC，
∵DE∥BC（画图），
∴∠2=∠B，∠1=∠C（两直线平行，内错角相等），
∴∠B+∠C+∠3=∠2+∠1+∠3=180°，
即∠BAC+∠B+∠C=180°．

点评：注意掌握作辅助线的叙述方法．