题目内容
【题目】阅读材料,解答下列问题.
例:当a>0时,如a=6,则|a|=|6|=6,故此时|a|是它本身;当a=0时,|a|=0,故此时|a|是零;
当a<0时,如a=﹣6,则|a|=|﹣6|=6=﹣(﹣6),故此时|a|是它的相反数.
综上所述,|a|可分三种情况,即|a|= 
这种分析方法渗透了数学的分类讨论思想.
问:
(1)请仿照例中的分类讨论的方法,分析二次根式 ![]() 的各种展开的情况.
的各种展开的情况.
(2)猜想 ![]() 与|a|的大小关系是
与|a|的大小关系是 ![]() |a|.
|a|.
(3)当1<x<2时,试化简: ![]() .
.
【答案】
(1)解:当a>0时,如a=3,则 ![]() ,故此时
,故此时 ![]() 的结果是它本身;
的结果是它本身;
当a=0时, ![]() =0,故此时
=0,故此时 ![]() 的结果是零;
的结果是零;
当a<0时,如a=﹣3,则 ![]() ,故此时
,故此时 ![]() 的结果是它的相反数.
的结果是它的相反数.
综上所述, ![]() 的结果可分三种情况,即
的结果可分三种情况,即 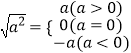
(2)=
(3)解:∵1<x<2,
∴x﹣1>0,x﹣2<0,
∴ ![]() =x﹣1+(2﹣x)
=x﹣1+(2﹣x)
=1.
【解析】(1)根据算术平方根的非负性知![]()
![]() 0,故一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;
0,故一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;
(2)根据绝对值的非负性知:一个正数的绝对值等于它本身,零的绝对值等于零,负数的绝对值等于它的相反数;根据算术平方根的非负性知:一个正数的平方的算术平方根等于它本身;0的平方的算术平方根等于它本身;一个负数的平方的算术平方根等于它的相反数;故![]() =|a|;
=|a|;
(3)因1<x<2,故x﹣1>0,x﹣2<0根据绝对值及算数平方根的意义,分别化简,再合并即可。

练习册系列答案
相关题目