��Ŀ����
����Ŀ�����������죩
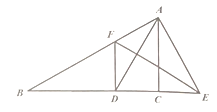
����1����ͼ1�����ı���ABCD�У�CB=CD����B=��ADC=90�㣬��BCD=120�㣮E��F�ֱ���AB��AD�ϵĵ㣮�ҡ�ECF=60�㣮̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG=BE������CG����֤����CBE�ա�CDG����֤����CEF�ա�CGF�����ó�����ȷ������ ��
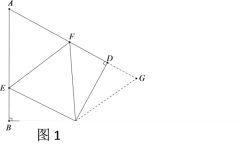
��̽��˼����
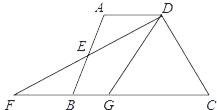
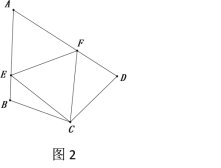
����2����ͼ2����������1��������Ϊ���ı���ABCD�У�CB=CD����ABC+��ADC=180�㣬��ECF=![]() ��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
����չ���죩
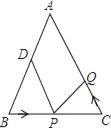
����3����ͼ3��������2�������£�����E��AB���ӳ����ϣ���F��DA���ӳ����ϣ���BE=2��DF=8����EF�ij�����ֱ��д���𰸣�
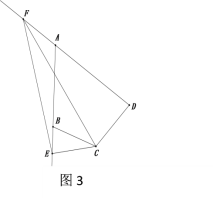
���𰸡���1��EF=BE+DF����2������1�н�����Ȼ����,���ɼ���������3��6.
��������
�ɡ�CEF�ա�CGF��֪CE=CG���ɡ�ECF=60�㣬��BCD=120���֤��FCG=60�㣬�Ӷ���֪��ECF�ա�FCG���ó�EF=GF���Ӷ��ó�EF=BE+DF��ͬ���ɵó���2����3����
��1��EF=BE+DF�����ɣ�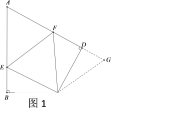
�ӳ�FD����G,ʹDG=BE,����CG��
�ڡ�CBE���CDG��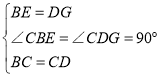
���CBE�ա�CDG��SAS����
��CE=CG����BCE=��DCG��
�ߡ�BCD=120�㣬
���ECG=120��
�ߡ�ECF=60�㣬
���ECF=��GCF��
�ڡ�CEF�͡�CGF��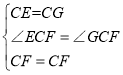 ,
,
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE
��2���⣺����1�н�����Ȼ����,��ͼ,
���ɣ��ӳ�FD����G.ʹDG=BE.����CG��
�ߡ�ABC+��ADC=180�㣬��CDG+��ADC=180�㣬
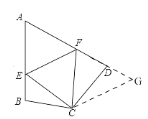
���ABC=��GDC,�ڡ�CBE�͡�CDG��,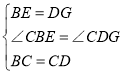
���CBE�ա�CDG(SAS)��
��CE=CG����BCE=��DCG��
���BCD=��ECG��
�ߡ�ECF=![]() ��BCD
��BCD
���ECF=![]() ��ECG
��ECG
���ECF=��GCF��
�ڡ�CEF�͡�CGF��,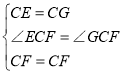
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE
��3��EF=6����Ϊ��ʱDF=EF+BE�����ɣ���ͼ3��
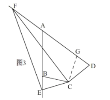
�ӳ�FD����G��ʹDG=BE������CG��
�ߡ�ABC+��ADC=180�㣬��CDG+��ADC=180�㣬
���ABC=��GDC���ڡ�CBE�͡�CDG��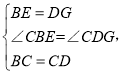 ���CBE�ա�CDG(SAS)��
���CBE�ա�CDG(SAS)��
��CE=CG����BCE=��DCG��
���BCD=��ECG��
�ߡ�ECF=![]() ��BCD
��BCD
���ECF=![]() ��ECG
��ECG
���ECF=��GCF��
�ڡ�CEF�͡�CGF��,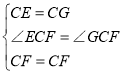
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE

 �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�