题目内容
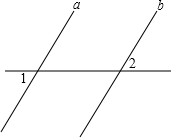
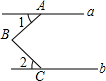
已知直线l1∥l2,且l3、l4和l1、l2分别交于A、B、C、D四点,点P在直线AB上.设∠ADP=∠1,∠DPC=∠2,∠BCP=∠3.
(1)探究∠1、∠2、∠3之间的关系下面给出推导过程,请你填写理由
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否会发生变化?
(3)如果点P在A、B两点外侧时,猜想∠1、∠2、∠3之间的数量关系(点P和A、B不重合),并说明理由.
(1)探究∠1、∠2、∠3之间的关系下面给出推导过程,请你填写理由
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否会发生变化?
(3)如果点P在A、B两点外侧时,猜想∠1、∠2、∠3之间的数量关系(点P和A、B不重合),并说明理由.
(1)证明:过点P作PE∥l1
∵PE∥l1(已作)
∴∠1=∠DPE(两直线平行,内错角相等)
∵PE∥l1,l1∥l2(已知)
∴PE∥l2(平行于同一条直线的两直线平行)
∴∠3=∠EPC(两直线平行,内错角相等)
∵∠2=∠DPE+∠EPC
∴∠2=∠1+∠3(等量代换)
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系不发生变化,
仍是∠2=∠1+∠3.
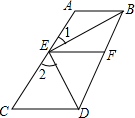
(3)如果点P在A、B两点外侧运动时,如图,可猜想∠1、∠2、∠3之间的关系是:∠1=∠2+∠3.
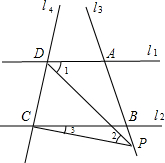
证明:如图,过点P作PE∥l1
∵PE∥l1(已作)
∴∠1=∠DPE(两直线平行,内错角相等)
∵PE∥l1,l1∥l2(已知)
∴PE∥l2(平行于同一条直线的两直线平行)
∴∠3=∠EPC(两直线平行,内错角相等)
∵∠1=∠DPC+∠EPC
∴∠1=∠2+∠3(等量代换).
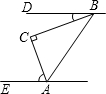
当P在A的上边时,同理可得∠3=∠1+∠2.
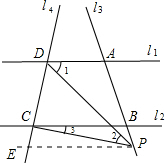
∵PE∥l1(已作)
∴∠1=∠DPE(两直线平行,内错角相等)
∵PE∥l1,l1∥l2(已知)
∴PE∥l2(平行于同一条直线的两直线平行)
∴∠3=∠EPC(两直线平行,内错角相等)
∵∠2=∠DPE+∠EPC
∴∠2=∠1+∠3(等量代换)
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系不发生变化,
仍是∠2=∠1+∠3.
(3)如果点P在A、B两点外侧运动时,如图,可猜想∠1、∠2、∠3之间的关系是:∠1=∠2+∠3.

证明:如图,过点P作PE∥l1
∵PE∥l1(已作)
∴∠1=∠DPE(两直线平行,内错角相等)
∵PE∥l1,l1∥l2(已知)
∴PE∥l2(平行于同一条直线的两直线平行)
∴∠3=∠EPC(两直线平行,内错角相等)
∵∠1=∠DPC+∠EPC
∴∠1=∠2+∠3(等量代换).
当P在A的上边时,同理可得∠3=∠1+∠2.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目