题目内容
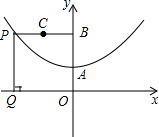 (2009•雅安)如图,抛物线的顶点A的坐标(0,2),对称轴为y轴,且经过点(-4,4).
(2009•雅安)如图,抛物线的顶点A的坐标(0,2),对称轴为y轴,且经过点(-4,4).(1)求抛物线的表达式.
(2)若点B的坐标为(0,4),P为抛物线上一点(如图),过点P作PQ⊥x轴于点Q,连接PB.求证:PQ=PB.
(3)若点C(-2,4),利用(2)的结论.判断抛物线上是否存在一点K,使△KBC的周长最小?若存在,求出这个最小值,并求此时点K的坐标;若不存在,请说明理由.
分析:(1)已知抛物线的顶点坐标,可将解析式设为y=a(x-k)2+h的形式,再将另一点的坐标代入即可确定待定系数.
(2)首先设P点的坐标,然后表示出PQ、PB的长,进行比较即可.
(3)BC的长是定值,若△KBC的周长最小,那么KC+KB的长最小,结合(2)的结论,当CK∥y轴,即过C作x轴的垂线时,该垂线和抛物线的交点即为符合条件的K点.
(2)首先设P点的坐标,然后表示出PQ、PB的长,进行比较即可.
(3)BC的长是定值,若△KBC的周长最小,那么KC+KB的长最小,结合(2)的结论,当CK∥y轴,即过C作x轴的垂线时,该垂线和抛物线的交点即为符合条件的K点.
解答:(1)解:由于抛物线的顶点为(0,2),设其解析式为:y=ax2+2;
将点(-4,4)代入上式,得:a×(-4)2+2=4,a=
即:抛物线的解析式:y=
x2+2.
(2)证明:设P(a,
a2+2),则PQ=
a2+2.
已知:B(0,4),则 PB=
=
a2+2;
即:PQ=PB.
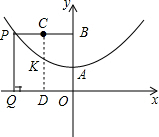 (3)解:如图,过C作CD⊥x轴于D,交抛物线于点K;
(3)解:如图,过C作CD⊥x轴于D,交抛物线于点K;
由于BC是定值,若△CKB的周长最小,那么 CK+KB 的值需最小.
由(2)知:KD=KB,则CD=CK+KD=CK+KB;
在抛物线上取K点外的任一点P,则:CD=CK+KD<CP+PQ,即:CK+KB<CP+BP
因此K点即为所求.
已知C(-2,4),将x=-2代入y=
x2+2中,得:y=
,即 K(-2,
).
△CKB的最小周长:CK+KB+CB=CD+BC=4+2=6.
将点(-4,4)代入上式,得:a×(-4)2+2=4,a=
| 1 |
| 8 |
即:抛物线的解析式:y=
| 1 |
| 8 |
(2)证明:设P(a,
| 1 |
| 8 |
| 1 |
| 8 |
已知:B(0,4),则 PB=
(a-0)2+(
|
| 1 |
| 8 |
即:PQ=PB.
 (3)解:如图,过C作CD⊥x轴于D,交抛物线于点K;
(3)解:如图,过C作CD⊥x轴于D,交抛物线于点K;由于BC是定值,若△CKB的周长最小,那么 CK+KB 的值需最小.
由(2)知:KD=KB,则CD=CK+KD=CK+KB;
在抛物线上取K点外的任一点P,则:CD=CK+KD<CP+PQ,即:CK+KB<CP+BP
因此K点即为所求.
已知C(-2,4),将x=-2代入y=
| 1 |
| 8 |
| 5 |
| 2 |
| 5 |
| 2 |
△CKB的最小周长:CK+KB+CB=CD+BC=4+2=6.
点评:该二次函数综合题主要考查了:函数解析式的确定、直角坐标系中两点间的距离公式等知识,难度适中.准确找出K点位置是解答(3)的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
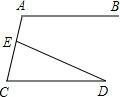 (2009•雅安)如图,AB∥CD,∠A=100°,∠D=25°,则∠AED=( )
(2009•雅安)如图,AB∥CD,∠A=100°,∠D=25°,则∠AED=( ) (2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=
(2009•雅安)如图,将△ABC沿BC方向平移得到△A′B′C′.已知BC=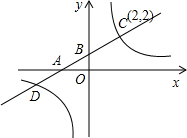 (2009•雅安)如图,一次函数y=kx+b的图象与反比例函数y=
(2009•雅安)如图,一次函数y=kx+b的图象与反比例函数y=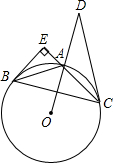 (2009•雅安)如图,△ABC内接于⊙O,过点B的切线与CA的延长线相交于点E,且∠BEC=90°,点D在OA的延长线上,AO⊥BC,∠ODC=30°.
(2009•雅安)如图,△ABC内接于⊙O,过点B的切线与CA的延长线相交于点E,且∠BEC=90°,点D在OA的延长线上,AO⊥BC,∠ODC=30°.