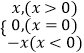Question

【题目】如图，在平面直角坐标系xOy中，已知正比例函数与一次函数的图象交于点A．

（1）求点A的坐标；

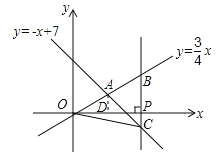
（2）设x轴上有一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交和的图象于点B、C，连接OC．若BC=OA，求△OBC的面积．

Answer 1

【答案】（1）A（4，3）；（2）28．

【解析】

试题分析：（1）联立两一次函数的解析式求出x、y的值即可得出A点坐标；

（2）过点A作x轴的垂线，垂足为D，在Rt△OAD中根据勾股定理求出OA的长，故可得出BC的长，根据P（a，0）可用a表示出B、C的坐标，故可得出a的值，由三角形的面积公式即可得出结论．

试题解析：（1）∵由题意得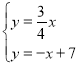，，解得：，∴A（4，3）；

（2）过点A作x轴的垂线，垂足为D，在Rt△OAD中，由勾股定理得，OA===5，

∴BC=OA=×5=7．∵P（a，0），∴B（a，），C（a，﹣a+7），∴BC==，∴=7，解得a=8，∴S△OBC=BCOP=×7×8=28．