题目内容
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE. 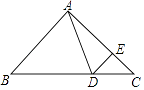
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
【答案】
(1)解:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=105°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC﹣∠EDC=105°﹣∠EDC=45°+∠EDC,
解得:∠CDE=30°
(2)解:∠CDE= ![]() ∠BAD,
∠BAD,
理由:设∠BAD=x,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=45°+x,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠CDE,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC﹣∠CDE=∠45°+x﹣∠CDE=45°+∠CDE,
得:∠CDE= ![]() ∠BAD
∠BAD
【解析】(1)先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+60°=105°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论;(2)利用(1)的思路与方法解答即可.

练习册系列答案
相关题目