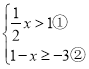题目内容
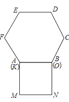
【题目】在平面直角坐标系中,抛物线G:![]() 与
与![]() 轴交于点C,抛物线G的顶点为D,直线
轴交于点C,抛物线G的顶点为D,直线![]() :
:![]() .
.
(1)当![]() 时,直接写出直线
时,直接写出直线![]() 被抛物线G截得的线段长;
被抛物线G截得的线段长;
(2)随着![]() 取值的变化,判断点C,D是否都在直线
取值的变化,判断点C,D是否都在直线![]() 上;
上;
(3)若直线被![]() 被抛物线G截得的线段长不小于
被抛物线G截得的线段长不小于![]() ,结合函数图像,直接写出m的取值范围.
,结合函数图像,直接写出m的取值范围.
【答案】(1)![]() ;(2)点D,C始终在直线
;(2)点D,C始终在直线![]() 上;(3)
上;(3)![]() 或
或![]() .
.
【解析】
(1)当m=1时,抛物线G的函数表达式为y=x2+2x,直线的函数表达式为y=x,求两函数的交点,即可求出抛物线G截得的线段的长;
(2)先求出C、D两点的坐标,再代入直线的解析式进行检验即可;
(3)先联立直线与抛物线的解析式,求出它们的交点坐标,再根据这两个交点之间的距离不小于2列出不等式,求解即可.
(1)当m=1时,抛物线G的函数表达式为y=x2+2x,直线的函数表达式为y=x,
联立得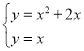 ,解得
,解得![]() 或
或![]() .
.
所以两函数的交点坐标为:![]() 和
和![]() ,
,
∴直线被抛物线G截得的线段长为![]() ;
;
(2)无论m取何值,点C,D都在直线上.理由如下:
∵抛物线G:y=mx2+2mx+m-1(m≠0)与y轴交于点C,
∴点C的坐标为C(0,m-1),
∵y=mx2+2mx+m-1=m(x+1)2-1,
∴抛物线G的顶点D的坐标为(-1,-1),
对于直线:y=mx+m-1(m≠0),
当x=0时,y=m-1,
当x=-1时,y=m·(-1)+m-1=-1,
∴无论m取何值,点C,D都在直线上;
(3)解方程组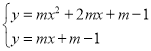 ,
,
得![]() ,或
,或![]() ,
,
∴直线与抛物线G的交点为(0,m-1),(-1,-1).
∵直线被抛物线G截得的线段长不小于![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 或
或![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.