题目内容
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于点C.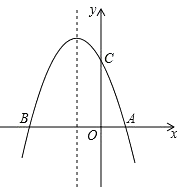
(1)求B、C两点的坐标;
(2)在该抛物线的对称轴上是否存在点P,使得△PAC的周长最小?若存在,求出点P的坐标;若不存在,请说明理由;
(3)抛物线在第二象限内是否存在一点Q,使△QBC的面积最大?,若存在,求出点Q的坐标及△QBC的面积最大值;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=﹣x2﹣2x+3与x轴交于A,B两点,与y轴交于点C,
当y=0时,即﹣x2﹣2x+3=0,
解得:x1=﹣3,x2=1,
当x=0时,y=3,
∴B(﹣3,0)、C(0,3)
(2)
解:存在;
如图1,∵抛物线的解析式为:y=﹣x2﹣2x+3,
∴抛物线的对称轴x=﹣1,C(0,3)
∴C′(﹣2,3),
设直线AC′的解析式为:y=kx+b,
∵A(1,0),
∴ ![]() 解得
解得 ![]() ,
,
∴直线AC′的解析式为:y=﹣x+1,
把x=﹣1代入直线AC′的解析式y=﹣x+1,得y=2,
∴P(﹣1,2)
(3)
解:存在;
如图2,设Q(m,﹣m2﹣2m+3),过Q作QP⊥x轴于P,
∴OP=﹣m,PQ=﹣m2﹣2m+3,BP=3+m,
∴S△PBQ= ![]() BPPQ=
BPPQ= ![]() (3+m)(﹣m2﹣2m+3),S四边形QPOC=
(3+m)(﹣m2﹣2m+3),S四边形QPOC= ![]() (OC+PQ)OP=
(OC+PQ)OP= ![]() (3﹣m2﹣2m+3)(﹣m),S△BOC=
(3﹣m2﹣2m+3)(﹣m),S△BOC= ![]() OBOC=
OBOC= ![]() ×3×3=
×3×3= ![]() ,
,
∴S△PBC=S△PBQ+S四边形QPOC﹣S△BOC=﹣ ![]() m2﹣
m2﹣ ![]() m,
m,
即S△PBC=﹣ ![]() m2﹣
m2﹣ ![]() m=﹣
m=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ,
,
∴当m=﹣ ![]() 时,△QBC的面积最大,最大值为
时,△QBC的面积最大,最大值为 ![]() ;
;
∴Q(﹣ ![]() ,
, ![]() ).
).

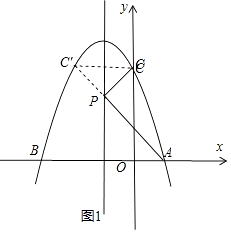
【解析】(1)根据抛物线与x轴的交点坐标与系数的关系即可求得;(2)根据轴对称的性质先找出C的对称点C′,然后连接AC′即可找到P点,最后根据A、C′的坐标求得直线AC′的解析式,即可求得P的坐标;(3)根据S△QBC=S△QBP+S四边形QPOC﹣S△BOC即可求得解析式,根据解析式即可求得求出点Q的坐标及△QBC的面积最大值;
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.

 培优三好生系列答案
培优三好生系列答案【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 12 | |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
【题目】某茶叶厂用甲,乙,丙三台包装机分装质量为200g的茶叶,从它们各自分装的茶叶中分别随机抽取了20盒,得到它们的实际质量的方差如下表所示:
甲包装机 | 乙包装机 | 丙包装机 | |
方差 | 10.96 | 5.96 | 12.32 |
根据表中数据,可以认为三台包装机中,包装茶叶的质量最稳定是_____.
【题目】A、B两仓库分别有水泥20吨和30吨,C、D两工地分别需要水泥15吨和35吨.已知从A、B仓库到C、D工地的运价如下表:
到C工地 | 到D工地 | |
A仓库 | 每吨15元 | 每吨12元 |
B仓库 | 每吨10元 | 每吨9元 |
(1)若从A仓库运到C工地的水泥为![]() 吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从A仓库运到C工地的水泥为15吨时,那么总运输费为多少元?