题目内容
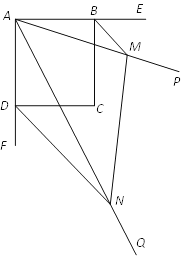
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
【答案】(1)证明见解析;(2)22.5°.
【解析】试题分析:(1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;
(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
试题解析:(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°-∠DAN,
∴△ABM∽△NDA;
(2)∵四边形BMND为矩形,
∴BM=DN,
∵△ABM∽△NDA,
∴![]() ,
,
∴BM2=AB2,
∴BM=AB,
∴∠BAM=∠BMA=![]()

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目