题目内容
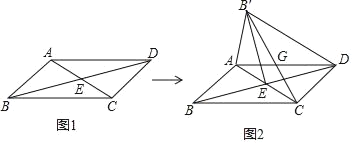
【题目】ABCD中,对角线AC与BD相交于点E,将△ABC沿AC所在直线翻折至△AB′C,若点B的落点记为B′,连接B′D、B′C,其中B′C与AD相交于点G.
①△AGC是等腰三角形;②△B′ED是等腰三角形;
③△B′GD是等腰三角形;④AC∥B′D;
⑤若∠AEB=45°,BD=2,则DB′的长为![]() ;
;
其中正确的有( )个.

A. 2B. 3C. 4D. 5
【答案】D
【解析】
利用平行四边形的性质、翻折不变性一一判断即可解决问题;
解:∵四边形ABCD是平行四边形,
∴BE=DE,AD∥BC,AD=BC,
∴∠GAC=∠ACB,
由翻折可知:BE=EB′=DE,∠ACB=∠ACG,CB=CB′,
∴∠GAC=∠ACG,
∴△AGC,△B′ED是等腰三角形,故①②正确,
∵AB′=AB=DC,CB′=AD,DB′=B′D,
∴△ADB′≌△CB′D,
∴∠ADB′=∠CB′D,
∴GD=GB′,
∴△B′GD是等腰三角形,故③正确,
∵∠GAC=∠GCA,∠AGC=∠DGB′,
∴∠GAC=∠GDB′,
∴AC∥DB′,故④正确.
∵∠AEB=45°,BD=2,
∴∠BEB′=∠DEB′=90°,
∵DE=EB′=1,
∴DB′=![]() ,故⑤正确.
,故⑤正确.
故选:D.

练习册系列答案
相关题目




