��Ŀ����
����Ŀ��(1)���ⷢ��
����ABC�У�AC=BC����ACB=������DΪֱ��BC��һ���㣬����D��DF��AC��AB�ڵ�F����AD�Ƶ�D˳ʱ����ת���õ�ED������BE��
��ͼ(1)������=90��ʱ���Բ��룺
��AF��BE��������ϵ���� �����ڡ�ABE=�� ����
(2)��չ̽��
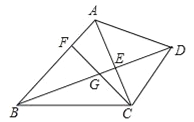
��ͼ(2)����0��<��<90��ʱ�����ж�AF��BE��������ϵ����ABE�Ķ�������˵�����ɣ�
(3)�������
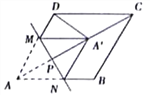
��ͼ(3)������ABC�У�AC=BC��AB=8����ACB=������D������BC�ϣ���AD�Ƶ�D˳ʱ����ת���õ�ED������BE����BD=3CDʱ����ֱ��д��BE�ij��ȣ�

���𰸡���1����AF��BF ��90������2��AF��BE����ABE���������ɼ���������3��2��4
��������
��1��������SAS����ADF�ա�EDB���ɵ�AF=BE���ڸ���������ȫ�ȿɵá�DAF����E������Ϊ��AOD����EOB��������á�ABE=��ADO=90����
��2�����ۣ�AF=BF����ABE=a������SAS��֤��ADF�ա�EDB�����ɽ�����⣻
��3���ֵ���D���߶�BC�Ϻ͵���D��BC���ӳ����������������ۣ�����ƽ���߷��߶γɱ�������⣮
��1������AB��DE��O��

�ߡ�ACB��90����AC��BC��
���ABC��45����
��DF��AC��
���FDB����C��90����
���DFB����DBF��45����
��DF��DB��
�ߡ�ADE����FDB��90����
���ADE-��FDE=��FDB-��FDE
���ADF����EDB��
��DA��DE��
���ADF�ա�EDB��
��AF��BE��
���ɢٵã���ADF�ա�EDB��
���DAF����E��
�֡ߡ�AOD����EOB��
���ABE����ADO��90����
�ʴ�Ϊ��AF��BF��90����
(2)���ۣ�AF��BE����ABE�������������£�
��DF��AC��
���ACB����FDB����ADE=������CAB����DFB��
��AC��BC��
���ABC����CAB��
���ABC����DFB��
��DB��DF��
�ߡ�ADF����ADE����FDE����EDB����FDB����FDE��
���ADF����EDB��
�֡�AD��DE��
���ADF�ա�EDB��
��AF��BE����AFD����EBD
�ߡ�AFD����ABC+��FDB����DBE����ABD+��ABE��
���ABE����FDB������
(3)����ͼ3��1�У�����D��BC��ʱ��

��BD=3CD
��![]()
��DF��AC��
��![]() =
=![]() ��
��
��AB��8��
��AF��2��
��(2)��֪��BE��AF��
��BE��AF��2��
����ͼ3��2�У�����D��BC���ӳ�����ʱ��

��BD=3CD
��![]()
��AC��DF��
��![]() ��
��![]() ��
��
��AB��8��
��AF��4��
��BE��AF��4
��BE�ij���Ϊ2��4��

����Ŀ��ij��˾����Ͳ�����������ʽ��������Ա�����ʶ�ȡ�ͣ������˷����ù�˾����10�����ţ��Ҹ����ŵ�������ͬ.Ϊ�˽���͵��˷����������10�������������ȡ��![]() �������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.
�������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.![]() .
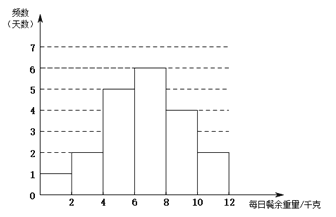
.![]() ����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺
����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ����
����
![]() .
.![]() ����ÿ�ղ���������
����ÿ�ղ���������![]() ��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() ����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() ����������20��������ÿ�ղ���������ƽ��������λ�����������£�
����������20��������ÿ�ղ���������ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
����������Ϣ���ش��������⣺
��1��д����![]() �е�ֵ��
�е�ֵ��
��2����![]() �����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������
�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������![]() ������
������![]() ������������____________��
������������____________��
��3�����![]() ����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.