题目内容
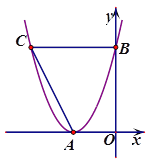
【题目】如图，已知抛物线与x轴只有一个交点A(－2，0)，与y轴交于点B(0，4).
（1）求抛物线对应的函数解析式；
（2）过点B做平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段（不含A、B两点）上，求四边形BMAC面积最大时，点M的坐标；
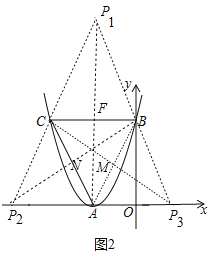
②在平面直角坐标系内是否存在点P，使以P、A、B、C为顶点的四边形是平行四边形，若存在直接写出所有满足条件的点P的坐标；若不存在，请说明理由.
【答案】（1）y＝(x＋2)2 （2）①点M的坐标为(－1，1) ②存在 所有满足条件的点P的坐标是(2，０)、(－6，０)、(－2，8)
【解析】（1）由已知可设抛物线对应函数的解析式为：y=a（x+2）2（a≠0），∵抛物线与y轴交于点B（0，4）
∴4=a（0+2）2
解得：a=1
∴抛物线对应的解析式为：y=（x+2）2．
（2）①如图1中，设点M的坐标为（m，（m+2）2），其中﹣2＜m＜0，则N点坐标（m，0）．
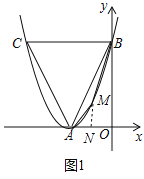
∵A、B、C是定点，∴若要四边形BMAC的面积最大，只要BMA的面积最大即可．
过M做MN⊥x轴于点N，则
S△AOB=
OAOB=×2×4=4
S△AMN=ANMN=×[m﹣（﹣2）]×（m+2）2=（m+2）3
S梯形ONMB=ON（MN+OB）
=×（﹣m）×[（m+2）2+4]
=﹣（m3+4m2+8m）
∴S△AMB=S△AOB﹣S△AMN﹣S梯形ONMB
=4﹣（m+2）3﹣[﹣（m3+4m2+8m）]
=﹣m2﹣2m，当m=﹣1时，S△AMB最大，∵（﹣1+2）2=1
∴此时点M的坐标为（﹣1，1）．
②存在．如图2中，∵四边形ABP1C是平行四边形，∴FC=FB，AF=FP1，∵B（0，4），C（﹣4，4），∴F（﹣2，4），设P1（x，y），则有
=﹣2，
=4，∴x=﹣2，y=8，∴P1（﹣2，8），同法可得P2（﹣6，0），P3（2，0）．
所有满足条件的点P的坐标是（2，0）、（﹣6，0）、（﹣2，8）．
