题目内容
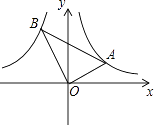
【题目】如图，在等边△ABC中，点D为边BC的中点，以AD为边作等边△ADE，连接BE．
求证：BE=BD．
【答案】证明：∵在等边△ABC中，点D为边BC的中点，
∴∠CAD=∠DAB= 
∠CAB=30°，
∵△ADE为等边三角形，
∴AD=AE，∠DAE=60°，
∵∠DAB=30°，
∴∠DAB=∠EAB=30°，
在△ADB与△AEB中，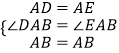 
，
∴△ADB≌△AEB（SAS），
∴BE=BD．
【解析】由等角三角形的三线合一得出∠CAD=∠DAB=30°，再由等边三角形的性质得出AD=AE，∠DAE=60°，进而判断出△ADB≌△AEB，再由三角形全等对应边相等得出结论。
【考点精析】通过灵活运用等边三角形的性质，掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
