题目内容
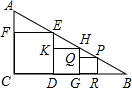如图，Rt△ABC中，∠C=90°，有三个正方形CDEF、DGHK、GRPQ，它们分别是△ACB、△EDB和△HGB的内接正方形，EF=10cm，HK=7cm，则第三个正方形的边长PQ的长（ ）分析：先由相似三角形的判定可得△QPH∽△KHE，再由相似三角形的性质可得QP：KH=QH：KE，然后将已知条件代入，即可求得PQ的长度．
解答：解：∵PQ∥HK，∴∠QPH=∠KHE，
又∵∠PQH=∠HKE=90°，
∴△QPH∽△KHE，
∴QP：KH=QH：KE，
设正方形GRPQ的边长为xcm．
又∵正方形CDEF的边长为10cm，正方形DGHK的边长为7cm，
∴x：7=（7-x）：3，
解得x=4.9．
故选D．
又∵∠PQH=∠HKE=90°，
∴△QPH∽△KHE，
∴QP：KH=QH：KE，
设正方形GRPQ的边长为xcm．
又∵正方形CDEF的边长为10cm，正方形DGHK的边长为7cm，
∴x：7=（7-x）：3，
解得x=4.9．
故选D．
点评：本题考查了相似三角形的判定及性质，正方形的性质，得到△QPH∽△KHE是解题的关键．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
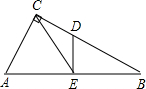如图，Rt△ABC中，∠ACB=90°，tanB=
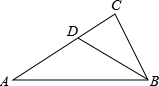如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ）
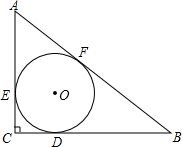如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
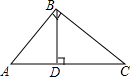如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．