题目内容
若反比例函数的图象经过点(1,-2),那么它一定经过( )
分析:根据反比例函数图象上点的坐标特征得到此反比例函数图象上点的横纵坐标之积为-2,然后分别计算四个选项中个点的横纵坐标之积,再进行判断.
解答:解:设反比例函数解析式为y=
,
∵反比例函数的图象经过点(1,-2),
∴k=-2×1=-2,
∵2×(-1)=-2,-
×2=-
,-2×(-5)=10,0×(-3)=0,
∴反比例函数的图象经过点(1,-2),它一定经过点(2,-1).
故选A.
| k |
| x |
∵反比例函数的图象经过点(1,-2),
∴k=-2×1=-2,
∵2×(-1)=-2,-
| 1 |
| 3 |
| 2 |
| 3 |
∴反比例函数的图象经过点(1,-2),它一定经过点(2,-1).
故选A.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=xk(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
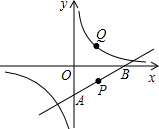 如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.
如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.