题目内容
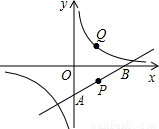
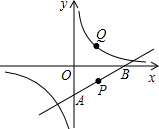 如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.
如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.分析:先根据待定系数法求出直线AB的解析式为y=
x-2,由于点P在直线AB上且纵坐标为-1,可确定P点坐标为(2,-1),而点P关于x轴的对称点为Q,根据关于x轴对称的点的坐标特点得到Q点的坐标为(2,1),然后再根据待定系数法求出过Q点的反比例函数解析式.
| 1 |
| 2 |
解答:解:设直线AB的解析式为y=kx+b,
把A(0,-2)和B(4,0)分别代入得
,
解得
,
∴直线AB的解析式为y=
x-2,
∵点P在直线y=
x-2上且y=-1,
∴把y=-1代入得x=2,
∴P点坐标为(2,-1),
∵点Q与点P关于x轴对称,
∴Q点的坐标为(2,1),
设反比例函数的解析式为y=
(k≠0),
把Q(2,1)代入得k=2×1=2,
所以经过点Q的反比例函数解析式为:y=
.
把A(0,-2)和B(4,0)分别代入得
|
解得
|
∴直线AB的解析式为y=
| 1 |
| 2 |
∵点P在直线y=
| 1 |
| 2 |
∴把y=-1代入得x=2,
∴P点坐标为(2,-1),
∵点Q与点P关于x轴对称,
∴Q点的坐标为(2,1),
设反比例函数的解析式为y=
| k |
| x |
把Q(2,1)代入得k=2×1=2,
所以经过点Q的反比例函数解析式为:y=
| 2 |
| x |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了待定系数法求函数的解析式以及关于x轴对称的点的坐标特点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
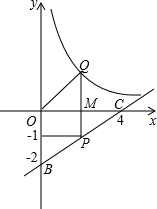 如图所示,点P在经过B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y=
如图所示,点P在经过B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y=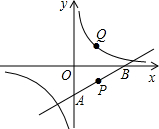 如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.
如图所示,点P在经过点A(0,-2),B(4,0)的直线上,且纵坐标为-1,点P关于x轴的对称点为Q.若反比例函数的图象经过点Q,则求其解析式.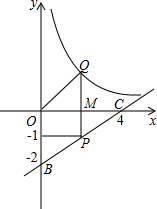 如图所示,点P在经过B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y=
如图所示,点P在经过B(0,-2),C(4,0)的直线上,且纵坐标为-1,Q点在y= (k>0)的图象上,且S△OMQ=
(k>0)的图象上,且S△OMQ= ,PQ∥y轴,求Q点的坐标.
,PQ∥y轴,求Q点的坐标.