题目内容
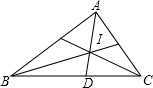 如图,I是△ABC的内心,∠A=40°,则∠CIB=
如图,I是△ABC的内心,∠A=40°,则∠CIB=分析:先求出∠B+∠C,再由内心的定义得出∠BIC=180°-
(∠B+∠C),从而得出答案.
| 1 |
| 2 |
解答:解:∵∠A=40°,
∴∠B+∠C=140°,
∵I是△ABC的内心,
∴∠BIC=180°-
(∠B+∠C)=180°-
×140°=110°.
故答案为:110°.
∴∠B+∠C=140°,
∵I是△ABC的内心,
∴∠BIC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:110°.
点评:本题考查了三角形内心的定义,是基础知识比较简单.

练习册系列答案
相关题目
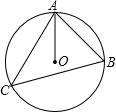 如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )
如图,⊙O是△ABC的外接圆,已知∠B=62°,则∠CAO的度数是( )| A、28° | B、30° | C、31° | D、62° |
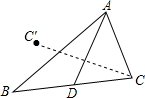 如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为
如图,AD是△ABC的中线,∠ADC=60°,点C′与点C关于直线AD对称,若BC=6cm,则点B与点C′之间的距离为 15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
15、如图,AD是△ABC的角平分线,∠B=60°,E,F分别在AC、AB上,且AE=AF,∠CDE=∠BAC,那么,图中长度一定与DE相等的线段共有
 如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( )
如图,⊙O是△ABC的外接圆,AB是直径,若∠B=50°,则∠A等于( ) 如图,AD是△ABC的外接圆直径,AD=
如图,AD是△ABC的外接圆直径,AD=