��Ŀ����
����Ŀ����ͼ������ABC�У���DΪBC�ߵ��е㣬�Ե�DΪ�������EDF�����߷ֱ����AB��AC���ڵ�E��F������EDF����A������
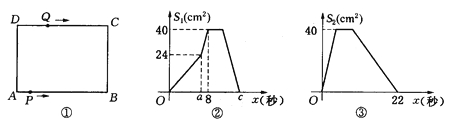
��1����ͼ1����AB=AC������A=90�������߶�DE��DF�к�������ϵ����ֱ��д�����ۣ�
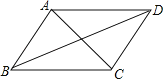
��2����ͼ2����AB=AC����ô��1���еĽ����Ƿ������������������֤����������������˵�����ɣ�
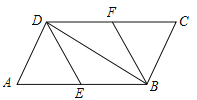
��3����ͼ3����AB��AC=m��n��̽���߶�DE��DF��������ϵ����֤����Ľ��ۣ�

���𰸡���1��DE=DF����2��DE=DF��Ȼ����������������3��������
��������
�����������1�����ȸ��ݵ��������ε����ʿɵ���DAB=��DAC=![]() ��BAC��AD��BC����֤����C=��B=45������ADE=��FDC��AD=DC��������ASA����֤����AED�ա�CFD�������õ�DE=DF��
��BAC��AD��BC����֤����C=��B=45������ADE=��FDC��AD=DC��������ASA����֤����AED�ա�CFD�������õ�DE=DF��
��2��DE=DF��Ȼ��������ͼ2������D��DM��AB��M����DN��AC��N������AD������EMD=��FND=90��������AB=AC����DΪBC�е㣬���������ε��������ߺ�һ�õ�ADƽ����BAC�����ǵõ�DM=DN�����ı���AMDN�У�����DMA=��DNA=90�����õ���MAN+��MDN=180������������EDF����MAN������֤����MDN=��EDF���Ƴ���DEM�ա�DFN��ASA�������ɵõ����ۣ�
��3������DE��DF=n��m����ͼ3������D��DM��AB��M����DN��AC��N������ADͬ��2����֤��1=��2��ͨ����DEM�ס�DFN���õ�![]() �����ڵ�EΪAC���е㣬�õ�S��ABD=S��ADC���еȻ�ʽ���ɵõ����ۣ�
�����ڵ�EΪAC���е㣬�õ�S��ABD=S��ADC���еȻ�ʽ���ɵõ����ۣ�
�⣺��1��DF=DE��
���ɣ���ͼ1������AD��
��Rt��ABC�ǵ��������Σ�
���C=��B=45����
��D��б��BC���е㣬
���DAB=��DAC=![]() ��BAC=45����AD��BC��
��BAC=45����AD��BC��
��AD=DC��
�ߡ�EDF=90����
���ADF+��ADE=90����
��AD��BC��
���ADC=90����
���ADF+��FDC=90����
���ADE=��FDC��
����ADE����CDF�� ��
��
���AED�ա�CFD��ASA����
��DE=DF��
��2��DE=DF��Ȼ������
��ͼ2������D��DM��AB��M����DN��AC��N������AD��
����EMD=��FND=90�㣬
��AB=AC����DΪBC�е㣬
��ADƽ����BAC��
��DM=DN��
�����ı���AMDN�У�����DMA=��DNA=90����
���MAN+��MDN=180����
���ߡ�EDF����MAN������
���MDN=��EDF��
���1=��2������DEM����DFN�� ��
��
���DEM�ա�DFN��ASA����
��DE=DF��
��3������DE��DF=n��m��
��ͼ3������D��DM��AB��M����DN��AC��N������AD��
ͬ��2����֤��1=��2��
���ߡ�EMD=��FND=90����
���DEM�ס�DFN��
��![]() ��
��
����DΪBC�ߵ��е㣬
��S��ABD=S��ADC��
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��