题目内容
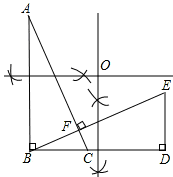
如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,
(1)求证:△ABC≌△BDE
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)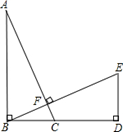
 AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,(1)求证:△ABC≌△BDE
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)

(1)见解析
(2)见解析
(2)见解析
三角形内角和定理,全等三角形的判定,作图(旋转变换),线段垂直平分线的性质。
(1)利用已知得出∠A=∠DBE,从而利用ASA得出△ABC≌△BDE即可。
证明:在Rt△ABC中,∵∠ABC=90°,∴∠ABE+∠DBE=90°。
∵BE⊥AC,∴∠ABE+∠A=90°。∴∠A=∠DBE。
∵DE是BD的垂线,∴∠D=90°。
在△ABC和△BDE中,∵∠A=∠DBE ,AB="DB" ,∠ABC=∠D,
∴△ABC≌△BDE(ASA)。
(2)利用垂直平分线的性质可以作出,或者利用正方形性质得出旋转中心也可。
如图,点O就是所求的旋转中心。
(1)利用已知得出∠A=∠DBE,从而利用ASA得出△ABC≌△BDE即可。
证明:在Rt△ABC中,∵∠ABC=90°,∴∠ABE+∠DBE=90°。
∵BE⊥AC,∴∠ABE+∠A=90°。∴∠A=∠DBE。
∵DE是BD的垂线,∴∠D=90°。
在△ABC和△BDE中,∵∠A=∠DBE ,AB="DB" ,∠ABC=∠D,
∴△ABC≌△BDE(ASA)。
(2)利用垂直平分线的性质可以作出,或者利用正方形性质得出旋转中心也可。
如图,点O就是所求的旋转中心。


练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
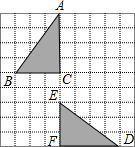


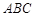 中,
中,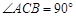 ,
,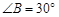 ,BC=2.三角板绕直角顶点
,BC=2.三角板绕直角顶点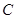 逆时针旋转,当点
逆时针旋转,当点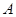 的对应点
的对应点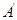 落在
落在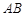 边上时即停止转动,则点
边上时即停止转动,则点 转过的路径长为 .
转过的路径长为 .