题目内容
(2012•金平区模拟)如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1=
,Sn=
(用含n的式子表示).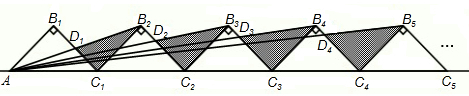
| 1 |
| 4 |
| 1 |
| 4 |
| n |
| 2(n+1) |
| n |
| 2(n+1) |

分析:连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1,依题意可知△B1C1B2是等腰直角三角形,知道△B1B2D1与△C1AD1相似,求出相似比,根据三角形面积性质可得S1S,同理:B2B3:AC2=1:2,所以B2D2:D2C2=1:2,所以S2=
×
=
,同样的道理,即可求出S3,S4…Sn.
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:∵n+1个边长为1的等腰三角形有一条边在同一直线上,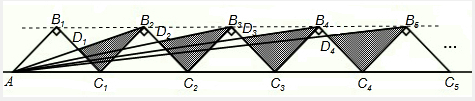
∴S△AB1C1=
×1×1=
,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=
×
=
,
故答案为:
;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=
×
=
,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=
×
=
,
∴S4=
×
=
,
…
∴Sn=
故答案为:
.

∴S△AB1C1=
| 1 |
| 2 |
| 1 |
| 2 |
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
∴S4=
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
…
∴Sn=
| n |
| 2(n+1) |
故答案为:
| n |
| 2(n+1) |
点评:本题主要考查相似三角形的判定和性质,等腰直角三角形的定义和性质、三角形的面公式等知识点、本题关键在于作好辅助线,得到相似三角形,求出相似比,就很容易得出答案了,意在提高同学们总结归纳的能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (2012•金平区模拟)如图,已知抛物线y=ax2+bx+2与x轴交于A(-4,0)、B(1,0)两点,与y轴交于点C.
(2012•金平区模拟)如图,已知抛物线y=ax2+bx+2与x轴交于A(-4,0)、B(1,0)两点,与y轴交于点C.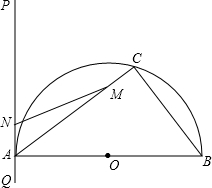 (2012•金平区模拟)如图,半圆O的直径AB=10,弦AC=8,过A作直线PQ,若∠PAC=∠ABC.
(2012•金平区模拟)如图,半圆O的直径AB=10,弦AC=8,过A作直线PQ,若∠PAC=∠ABC.