题目内容
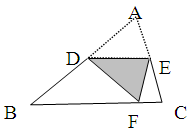
如图，在△ABC中，AD平分∠BAC，AB=AC-BD，则∠B:∠C=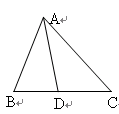 
2：1
解：如图，在AC上截取AE=AB，连接DE，
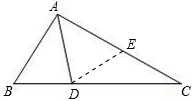
∵AD平分∠BAC，
∴∠BAD=∠EAD，
而AD是公共边，
∴△ABD≌△ADE，
∴∠B=∠AED，DE=BD，
AB-AC=BD，
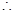AB+BD=AC=AE+CE，
∴DE=CE，
∴∠EDC=∠C，
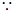∠AED=∠C+∠EDC=2∠C，
∴∠B=2∠C，
∴∠B：∠C=2：1.
∵AD平分∠BAC，
∴∠BAD=∠EAD，
而AD是公共边，
∴△ABD≌△ADE，
∴∠B=∠AED，DE=BD，
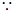AB-AC=BD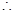，AB+BD=AC=AE+CE，∴DE=CE，
∴∠EDC=∠C，
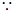∠AED=∠C+∠EDC=2∠C，∴∠B=2∠C，
∴∠B：∠C=2：1.
练习册系列答案
阅读快车系列答案
相关题目
