Question

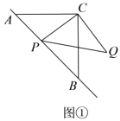
【题目】如图，已知等边△ABC，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F.

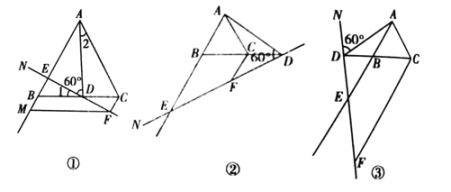
（1）当点D在线段BC上，∠NDB为锐角时，如图①.

①判断∠1与∠2的大小关系，并说明理由；

②过点F作FM∥BC交射线AB于点M，求证：CF+BE=CD；

（2）①当点D在线段BC的延长线上，∠NDB为锐角时，如图②，请直接写出线段CF，BE，CD之间的数量关系；

②当点D在线段CB的延长线上，∠NDB为钝角或直角时，如图③，请直接写出线段CF，BE，CD之间的数量关系.

Answer 1

【答案】（1）①∠1=∠2，理由见解析，②证明见解析；（2）①BE=CD+CF，②CF=CD+BE．

【解析】

（1）①由等边三角形的性质和∠ADN=60°，易得∠1+∠ADC=120°，∠2+∠ADC=120°，所以∠1=∠2；

②由条件易得四边形BCFM为平行四边形，得到BM=CF，BC=MF，再证明△MEF≌△CDA，得到ME=CD，利用等量代换即可得证；

（2）①过F作FH∥BC，易得四边形BCFH为平行四边形，可得HF=BC，BH=CF，然后证明△EFH≌△DAC，得到CD=EH，利用等量代换即可得BE=CD+CF；

②过E作EG∥BC，易得四边形BCGE为平行四边形，可得EG=BC，BE=CG，然后证明△EFG≌△ADC，得到CD=FG，利用等量代换即可得CF=CD+BE．

（1）①∠1=∠2，理由如下：

∵△ABC为等边三角形

∴∠ACB=60°

∴∠2+∠ADC=120°

又∵∠AND=60°

∴∠1+∠ADC=120°

∴∠1=∠2

②∵MF∥BC，CF∥BM

∴四边形BCFM为平行四边形

∴BM=CF，BC=MF=AC，

∵BC∥MF

∴∠1=∠EFM=∠2，∠EMF=∠ABC=60°

在△MEF和△CDA中，

∵∠EFM=∠2，MF= AC，∠EMF=∠ACD=60°

∴△MEF≌△CDA（ASA）

∴ME=CD

∴ME=BM+BE=CF+BE=CD

即CF+BE=CD

（2）①BE=CD+CF，证明如下：

如图，过F作FH∥BC，

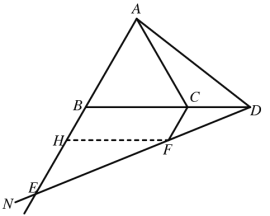
∵CF∥BH，FH∥BC，

∴四边形BCFH为平行四边形

∴HF=BC=AC，BH=CF

∵△ABC为等边三角形

∴∠ABC=∠ACB=60°

∴∠CAD+∠ADC=60°，∠DBE=120°，∠ACD=120°

又∵∠AND=60°，即∠BDN+∠ADC=60°

∴∠CAD=∠BDN

∵BD∥HF

∴∠HFE=∠BDN=∠CAD，∠EHF=∠ACD=120°

在△EFH和△DAC中，

∵∠EHF=∠ACD，HF=AC，∠HFE=∠CAD

∴△EFH≌△DAC（ASA）

∴EH=CD

∴BE=BH+EH=CF+CD

即BE=CD+CF；

②CF=CD+BE，证明如下：

如图所示，过E作EG∥BC，

∵EG∥BC，CG∥BE

∴四边形BCGE为平行四边形，

∴EG=BC=AC，BE=CG，

∵∠AND=60°，∠ACD=60°

∴∠ADC+∠CDE=120°，∠ADC+∠DAC=120°

∴∠CDE=∠DAC

又∵CD∥EG

∴∠GEF=∠CDE=∠DAC，∠EGF=∠DCF

∵AE∥CF

∴∠DCF=∠ABC=60°

∴∠EGF=∠ABC=60°

在△EFG和△ADC中，

∵∠GEF=∠DAC，EG=AC，∠EGF=∠ACD=60°

∴△EFG≌△ADC（ASA）

∴FG=CD

∴CF=CG+FG=BE+CD

即CF=CD+BE