题目内容
【题目】有两个函数![]() 和
和![]() ,若对于每个使函数有意义的实数
,若对于每个使函数有意义的实数![]() ,函数
,函数![]() 的值为两个函数值中中较小的数,则称函数
的值为两个函数值中中较小的数,则称函数![]() 为这两个函数
为这两个函数![]() 、
、![]() 的较小值函数。例如:
的较小值函数。例如:![]() ,
,![]() ,则
,则![]() 、
、![]() 的较小值函数
的较小值函数![]()
(1)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数;
的较小值函数;
①在如图的平面直角坐标系中画出函数![]() 的图像.
的图像.
②写出函数![]() 的两条性质.
的两条性质.
(2)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数,当
的较小值函数,当![]() 时,函数值
时,函数值![]() 的取值范围为
的取值范围为![]() .当
.当![]() 取某个范围内的任意值时,
取某个范围内的任意值时,![]() 为定值.直接写出满足条件的
为定值.直接写出满足条件的![]() 的取值范围及其对应的
的取值范围及其对应的![]() 值.
值.
(3)函数![]() 是函数
是函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() )的较小值函数,当
)的较小值函数,当![]() 时,随着
时,随着![]() 的增大,函数值
的增大,函数值![]() 先增大后减小,直接写出
先增大后减小,直接写出![]() 的取值范围.
的取值范围.

【答案】(1)①答案如图见解析;②答案不唯一,例如:当![]() 时,函数有最大值
时,函数有最大值![]() ;在每个象限内,随着
;在每个象限内,随着![]() 的增大,
的增大,![]() 先增大后减小;(2)当
先增大后减小;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)①分别画出两个函数![]() ,
,![]() 的图象,然后求出交点坐标,结合图象,两个函数图象中下方的部分保留,上方部分去掉即可的出函数y的图象.
的图象,然后求出交点坐标,结合图象,两个函数图象中下方的部分保留,上方部分去掉即可的出函数y的图象.
②结合图象针对函数的增减性和最值等写出两条性质即可.
(2)画出函数y的图象,计算出当x=![]() 时y=
时y=![]() ,根据对称性可知当x=
,根据对称性可知当x=![]() 时y=
时y=![]() ,然后结合图象即可得出a的范围和相应的b的值;
,然后结合图象即可得出a的范围和相应的b的值;
(3)结合函数的图象,分m>0和m<0两种情况进行讨论即可.
(1)①答案如图.
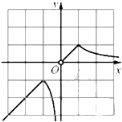
②答案不唯一,例如:当![]() 时,函数有最大值
时,函数有最大值![]() ;在每个象限内,随着
;在每个象限内,随着![]() 的增大,
的增大,![]() 先增大后减小;
先增大后减小;
(2)画出函数图象,如图所示:
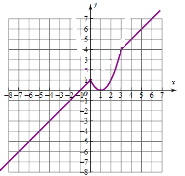
当x=![]() 时y=
时y=![]() ,根据对称性可知当x=
,根据对称性可知当x=![]() 时y=
时y=![]() ,
,
结合图象可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(3)当m>0时,画出函数y的图象如图所示:
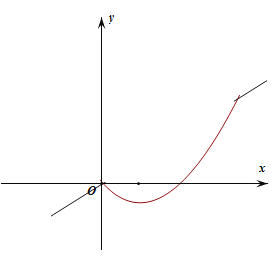
由图可知随着x的增大,函数值y先增大后减小时,
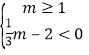 ,
,
解得:1≤m<6;
当m<0时,函数y的图像如图所示:
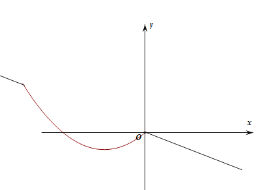
由图可知随着x的增大,函数值y先增大后减小时,
![]() ,
,
解得:m≤-3.
综上,![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目