题目内容
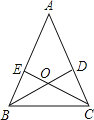
【题目】如图,△ABC中,AB=AC,两条角平分线BD、CE相交于点O.
(1)证明:△ABD≌△ACE;(2)证明:OB=OC.
【答案】见解析
【解析】试题分析:(1)、根据等腰三角形的性质和角平分线的性质得出∠ABD=∠ACE,然后结合∠A=∠A,AB=AC,根据ASA来判定两个三角形全等;(2)、根据等腰三角形和角平分线的性质得出∠DBC=∠ECB,从而得到△OBC为等腰三角形,从而得出答案.
试题解析:(1)证明:∵AB=AC,
∴∠ABC=∠ACB
∵两条角平分线BD、CE相交于点O
∴∠ABD=∠ACE,
在△ABD和△ACE中,
∠ABD=∠ACE,AB=AC,∠A=∠A,
△ABD≌△ACE.
(2)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵两条角平分线BD、CE相交于点O
∴∠DBC=∠ECB
∴OB=OC

练习册系列答案
相关题目