题目内容
【题目】如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1 , △B3D2C2的面积为S2 , …,△Bn+1DnCn的面积为Sn , 则S1= , Sn=(用含n的式子表示).
【答案】![]() ;
;![]()
【解析】解:∵n+1个边长为1的等腰三角形有一条边在同一直线上, ∴S△AB1C1= ![]() ×1×1=
×1×1= ![]() ,
,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1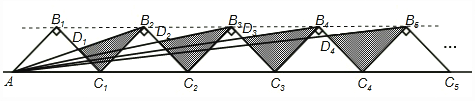
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1 ,
∴B1D1:D1C1=1:1,
∴S1= ![]() ×
× ![]() =
= ![]() ,所以答案是:
,所以答案是: ![]() ;
;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2= ![]() ×
× ![]() =
= ![]() ,
,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3= ![]() ×
× ![]() =
= ![]() ,∴S4=
,∴S4= ![]() ×
× ![]() =
= ![]() ,
,
…
∴Sn= ![]() 所以答案是:
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.

练习册系列答案
相关题目





