题目内容
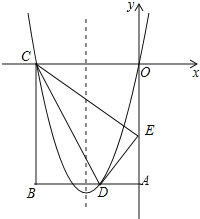
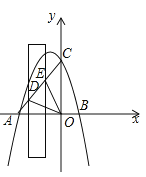
【题目】如图,抛物线![]() 与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,连结AC,现有一宽度为1,且长与y轴平行的矩形沿x轴方向平移,交直线AC于点D和E,△ODE周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
作正方形AOCM,连接OM、作MN∥AC,使得MN=DE,连接ON交AC于E,此时OD+OE的值最小.
解:如图,
当![]() 时,
时,
解之得
x1=-3,x2=1,
∴A(-3,0),B(1,0),
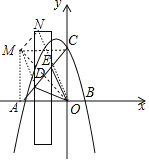
∵OA=OC=3,作正方形AOCM,连接OM、作MN∥AC,使得MN=DE,连接ON交AC于E,此时OD+OE的值最小.
∵MN=DE,MN∥DE,
∴四边形MNED是平行四边形,
∴DM=EN,
∴△ODE的周长=OD+DE+EO=DM+DE+OE=NE+OE+DE=ON+DE,
∵AC⊥OM,
∴MN⊥OM,
∴∠NMO=90°,
∵MN=DE=![]() ,OM=3
,OM=3![]() ,
,
∴ON=![]() ,
,
∴△ODE的周长的最小值为![]() ,
,
故选:A.

练习册系列答案
相关题目