Question

【题目】如图，抛物线y=x2﹣2x﹣8交y轴于点A，交x轴正半轴于点B．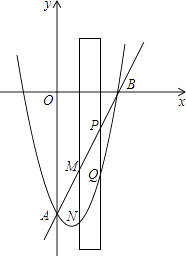

（1）求直线AB对应的函数关系式；
（2）有一宽度为1的直尺平行于y轴，在点A、B之间平行移动，直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ，设M点的横坐标为m，且0＜m＜3．试比较线段MN与PQ的大小．

Answer 1

【答案】
（1）

解：当x=0时，y=﹣8；当y=0时，x2﹣2x﹣8=0，

解得，x1=4，x2=﹣2；则A（0，﹣8），B（4，0）；

设一次函数解析式为y=kx+b，

将A（0，﹣8），B（4，0）分别代入解析式得 ；

解得， ．

故一次函数解析式为y=2x﹣8；

（2）

解：∵M点横坐标为m，则P点横坐标为（m+1）；

∴MN=（2m﹣8）﹣（m2﹣2m﹣8）=2m﹣8﹣m2+2m+8=﹣m2+4m；

PQ=[2（m+1）﹣8]﹣[（m+1）2﹣2（m+1）﹣8]=﹣m2+2m+3；

∴MN﹣PQ=（﹣m2+4m）﹣（﹣m2+2m+3）=2m﹣3；

①当2m﹣3=0时，m= ，即MN﹣PQ=0，MN=PQ；

②当2m﹣3＞0时， ＜m＜3，即MN﹣PQ＞0，MN＞PQ；

③当2m﹣3＜0时，0＜m＜ ，即MN﹣PQ＜0，MN＜PQ．

【解析】（1）利用二次函数解析式，求出A、B两点的坐标，再利用待定系数法求出一次函数解析式；（2）根据M的横坐标和直尺的宽度，求出P的横坐标，再代入直线和抛物线解析式，求出MN、PQ的长度表达式，再比较即可．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．