题目内容
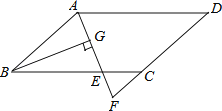
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
A.8 B.9.5 C.10 D.11.5
【答案】A
【解析】
试题分析:本题意在综合考查平行四边形、相似三角形、和勾股定理等知识的掌握程度和灵活运用能力,同时也体现了对数学中的数形结合思想的考查.在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,可得△ADF是等腰三角形,AD=DF=9;△ABE是等腰三角形,AB=BE=6,所以CF=3;在△ABG中,BG⊥AE,AB=6,BG=![]() ,可得AG=2,又△ADF是等腰三角形,BG⊥AE,所以AE=2AG=4,所以△ABE的周长等于16,又由ABCD可得△CEF∽△BEA,相似比为1:2,所以△CEF的周长为8,因此选A.
,可得AG=2,又△ADF是等腰三角形,BG⊥AE,所以AE=2AG=4,所以△ABE的周长等于16,又由ABCD可得△CEF∽△BEA,相似比为1:2,所以△CEF的周长为8,因此选A.
解:∵在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴AD=FD,
∴△ADF是等腰三角形,
同理△ABE是等腰三角形,
AD=DF=9;
∵AB=BE=6,
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG=![]() ,可得:AG=2,
,可得:AG=2,
又BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵ABCD
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故选:A.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目