题目内容
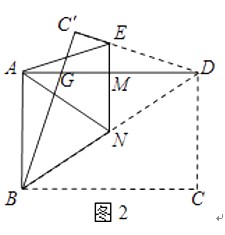
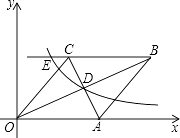
【题目】如图,在三角形ABC中, ∠B=60°, ∠C=![]() ,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
,点D是AB上一点,点E是AC上一点, ∠ADE=60°, 点F为线段BC上一点,连接EF,过D作DG//AC交EF于点G,
(1)若![]() =40°,求∠EDG的度数;
=40°,求∠EDG的度数;
(2)若∠FEC=2∠DEF,∠DGF=![]() ∠BFG,求
∠BFG,求![]() .
.

【答案】(1)40°;(2)72°
【解析】
(1)根据同位角相等即可判断出DE∥BC,根据平行线的性质即可求解;
(2)设∠DEF=x°,∠FEC=2x°,根据平行线的性质得∠DGE=∠FEC=2x° ,DEF=∠EFC=x°,分别表示出∠DGF、∠BFG,可得关于x的方程,解方程求得x的值,由三角形的内角和即可求解.
(1)∵∠B=∠ADE=60°
∴DE∥BC
∴∠C=∠AED=40°
又DG∥AC
∴∠GDE=∠AED=40°;
(2)∵∠FEC=2∠DEF
∴设∠DEF=x°,∠FEC=2x°
∵DG∥BC
∴∠DGE=∠FEC=2x°
∴∠DGF=(180-2x)°
又DE∥BC
∴∠DEF=∠EFC=x°
∴∠BFG=(180-x)°
又∠DGF=![]() ∠BFG
∠BFG
∴180-2x=![]() (180-x)
(180-x)
∴x=36,
∴∠EFC=x°=36°,∠FEC=2x°=72°,
∴∠C=α=180°-∠EFC -∠FEC =72°.
故答案为:(1)40°;(2)72°.

练习册系列答案
相关题目