题目内容
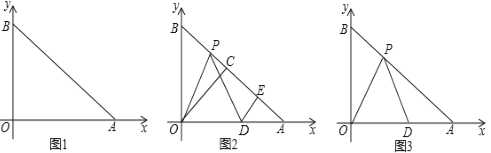
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为 . 
【答案】![]()
【解析】解:∵点A的坐标为(1,0),点D的坐标为(0,3),
∴OA=1,OD=3,
∵∠AOD=90°,
∴AD= ![]() =
= ![]() ,∠ODA+∠OAD=90°,
,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,AB=AD= ![]() ,
,
∴∠ODA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴ ![]() ,即
,即 ![]() ,解得:BA1=
,解得:BA1= ![]() ,
,
∴CA1= ![]() ,
,
同理,可得:C1A2= ![]() ,
,
∴第4个正方形的边长为 ![]() =
= ![]() ,
,
故答案为: ![]() .
.
先利用勾股定理求出AD的长,根据正方形的性质,可得出AB、BC的长。再证明△ABA1∽△DOA,求出CA1的长,按同样的方法求出C1A2的长、C2A3的长,观察规律得出第4个正方形的边长。

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】对某市中学生的幸福指数进行调查,从中抽取部分学生的调查表问卷进行统计,并绘制出不完整的统计表和条形统计图。
等级 | 频数 | 频率 |
★ | 60 | |
★★ | 80 | |
★★★ | 0.16 | |
★★★★ | 0.30 | |
★★★★★ |

(1)直接补全统计表;
(2)补全条形统计图(不要求写出计算过程);
(3)抽查的学生约占全市中学生的5%,估计全市约有多少名学生的幸福指数能达到五★级?